Основы программирования на языке Паскаль

Применим метод трапеций, суть которого заключается в том, что область делится на ряд трапеций, площади которых вычисляются и суммируются. Чем на большее количество трапеций мы разделим область, тем точнее получим результат (см.рис.4.2).

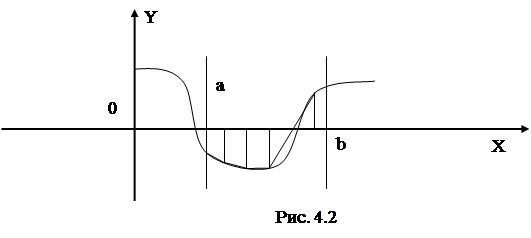
Program Prim14;

Var i,n:integer; a,b,x,h,s:real;

BEGIN writ

eln(' введите к-во точек разбиения n и величины а, b');

readln(n,a,b);

h:=(b-a)/n; s:=0; x:=a;

for i:=1 to n do

Begin s:=s+(abs(cos(x))+abs(cos(x+h)))/2*h;

x:=x+h; end;

writeln('s=',s);

readln; END.

Замечание: при вычислении S (так как функция пересекает ось OX) часть площадей может иметь отрицательное значение, поэтому мы берем abs(f(x)).

Усложним задачу: пусть нужно найти площадь криволинейной трапеции (интеграл), где функция от точки а до b sin(x), а после b до с cos(x).

Program Prim15;

Var i,n:integer; a,b,c,x,h,s,fxpred,fxposl:real;

BEGIN writeln('введите к-во точек разбиения n и величины а, b, c');

readln(n,a,b,c);

h:=(c-a)/n; s:=0; x:=a;

for i:=1 to n do

Begin

{ определимся, по какой из функций считать стороны трапеций }

if (x>=a) and (x<=b) then fxpred:= abs(sin(x)) else

fxpred:=abs(cos(x));

if (x+h>=a) and (x+h<=b) then fxposl:= abs(sin(x+h)) else

fxposl:=abs(cos(x+h));

s:=s+(fxpred+fxposl)/2*h;

x:=x+h; end;

writeln('s=',s);

readln; END.

В последних двух программах мы заменяем площадь криволинейной трапеции (интеграл) суммой трапеций. При этом нам неизвестно, какую ошибку мы допустим; знаем, что чем больше точек разбиения, тем точнее будет результат. Поставим задачу: совершенно точно знать, что мы посчитаем интеграл с точностью не менее заданной, например, что разность между площадью криволинейной трапеции и суммой прямоугольных трапеций будет не больше Е = 0.01. Для этого нам нужно посчитать результат для количества точек, например 10, затем – 100. Сравнить величины площадей, и, если их разность будет меньше Е, то можно с уверенностью сказать, что площадь для разбиения на 100 интервалов будет найдена с точностью не менее Е. Если разность между расчетами на 10 и 100 интервалов больше Е, то следует разбить область интегрирования на 1000 интервалов и сравнить сумму для 100 интервалов с суммой для 1000 интервалов, и если их разница будет меньше Е, то за результат принять площадь, посчитанную для 1000 разбиений и т.д. рано или поздно мы получим искомый результат. Сравнения сумм площадей трапеций будем производить с помощью оператора if.

Пусть функция будет cos(x). Напишем программу:

Program Prim16;

Label NAH,KON;

Var i,n:integer; a,b,x,h,spred,spos,e:real;

BEGIN writeln('введите точность е и границы a, b');

readln(e,a,b); spred:=9.9e+10; h:=0; n:=10;

NAH: spos:=0; h:=(b-a)/n; x:=a;

for i:=1 to n do

Begin spos:=spos+(abs(cos(x))+abs(cos(x+h)))/2*h;

x:=x+h; end;

if abs(spos-spred)<=e then Begin

writeln('s=',spos,' n=',n); goto KON; end

else spred:=spos; n:=n*10; x:=a; goto nah;

KON: readln; END.

Работа программы: for i: = i to n do, в первый раз оператор

Spоs: = spos+(abs(cos(x))+abs(cos(x+h)))/2*h

посчитает значение интеграла для 10 точек разбиения. Затем if сравнит полученное значение spos с 9.9Е+10. Конечно, разница между этими величинами не будет меньше е, тогда мы забудем число 9.9Е+10, так как присвоим spred: = spоs, чтобы при следующем выполнении if сравнивать предыдущее и последующее значения интеграла. После этого увеличим количество точек разбиения n: = n*10 и вернемся на начало вычисления spos, т.е. интеграла для 100 интервалов goto nach. После нового вычисления spos сравним 100 интервалов для 10 интервалов spred. Если разность между ними не меньше Е, то забудем значение s для 10 интервалов и занесем в spred значение для 100 интервалов. Затем вычислим значение интеграла для разбиения 1000 и результат занесем в spos, сравним spred и spos и т.д.

4.2. Оператор repeat. Общий вид

В отличие от for, оператор repeat (а также while) применяют тогда, когда неизвестно точно, сколько раз будет выполняться тело цикла. Общий вид оператора

repeat

оператор;

оператор;

– – – – – – – –

оператор until булевское выражение;

Работа оператора. Сначала выполняются операторы, составляющие тело цикла, затем выполняется булевское выражение, и если оно ложно, вновь выполняется тело цикла. Выход из цикла происходит, когда булевское выражение станет истинным.

Явного перебора параметров в repeat не предусмотрено, поэтому изменение параметров осуществляется в теле цикла. Здесь же мы должны позаботиться , чтобы рано или поздно булевское выражение стало истиной.

Замечания: 1.Тело оператора repeat выполняется по меньшей мере один раз. Оператор repeat еще называют циклом с послеусловием.

2. Перед until ';' не ставится.

Пример: найти сумму четных чисел в интервале от 0 до 100.

Program Prim17;

Var i,s:integer;

BEGIN i:=0; s:=0;

repeat

i:=i+2; s:=s+i

until i>100;

writeln('s=',s);

readln; END.

Пример: найти ток в цепи переменного тока в зависимости от частоты тока. Известно, что при последовательном соединении активной, емкостной и индукционной нагрузок сила тока может быть вычислена по формуле

Пусть U = 220, R = 100, L = 0.57, С = 3.2*10-3, Fначальное=10; F будем менять с шагом 0.5. Печатать все результаты. Результаты, когда i>3, нас не интересуют.

ProgramPrim18;

Var i,r,f,l,c,u:real;

BEGIN writeln(' введите значения u r l c');

readln(u,r,l,c);

f:=50;

repeat i:=u/sqrt(sqr(r)+sqr(2*pi*f*l-1/(2*pi*f*c)));

f:=f-1;

writeln('f=',f,' i=',i)

until i>3;

readln; END.

4.3. Оператор While

Оператор While цикла с предусловием.

While – булевское выражение; do – тело цикла.

Работа оператора. Вначале вычисляется булевское выражение, и если оно истинно, то выполняется тело цикла; если оно ложно, то происходит выход из цикла.

Тело цикла – один оператор, как правило, составной. Мы должны позаботиться о том, чтобы булевское выражение в теле цикла на каком-то этапе стало ложным, иначе цикл никогда не закончится. Цикл можно сделать умышленно бесконечным, написав: while true do оператор;

 Скачать реферат