Составление стоимостного межотраслевого баланса

1) Матричные вычисления произведем с помощью пакета Excel. Итак, матрицы

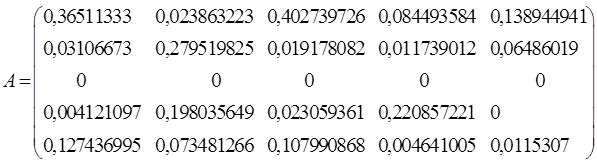
Матрица полных затрат

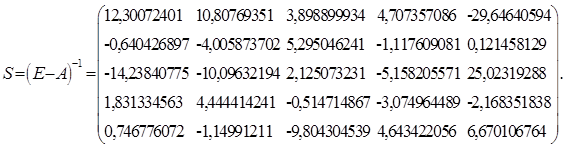
По условию задачи, спрос по всем отраслям должен увеличиться на 8%, т.е. вектор

конечного продукта должен стать

межотраслевой баланс равновесный цена затраты

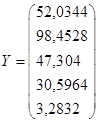
Тогда искомый вектор валового выпуска

Составим новую матрицу межотраслевого баланса (с точностью до второго знака после запятой). Для этого воспользуемся формулами

;

;

;

Промежуточные вычисления (с точностью до 2-го знака после запятой

=

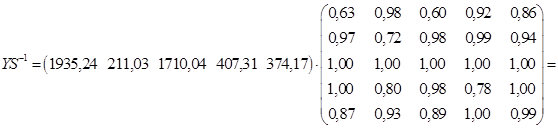
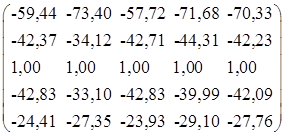
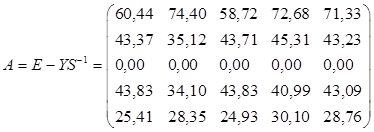
После чего новая матрица межотраслевого баланса будет выглядеть

2) Проследить эффект распространения, вызванный увеличением спроса на продукцию тяжелой промышленности дополнительно на 6%, т.е. конечный продукт станет равным

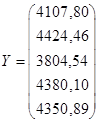
В результате этого изменения эффект распространения будет заключаться в том, что новый вектор валового выпуска будет иметь вид

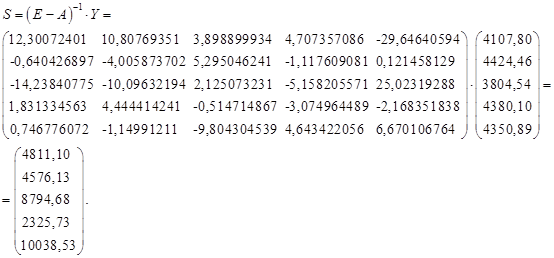
Для нахождения эффекта распространения привлечем уравнение для цен

P = AT P + v, откуда P = (E – AT)-1v.

Обратная матрица Леонтьева (E – AT)-1 – ценовой матричный мультипликатор – матричный мультипликатор ценового эффекта распространения.

Этот мультипликатор эффекта распространения найдем с помощью пакета Excel, сначала транспонируя матрицу А, затем отнимая ее от единичной матрицы и находя обратную матрицу. Проводя эти вычисления, получим

.

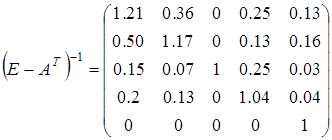Этот результат в качестве промежуточного будет использован в следующем пункте при расчете равновесной цены.

3) Отношение vj = Vj/Xj – называют долей добавленной стоимости, а вектор v = (v1,…,vn) – вектор долей добавленной стоимости. В матричном виде уравнение для цен будет иметь следующий вид

P = AT P + v

Решая уравнение это относительно Р, получим

P = (E – AT)-1v

По условию задачи, вектор

v = (0,5, 0,517, 0,499, 0,345, 0,547)

Тогда, с помощью пакета Excel, найдем равновесные цены

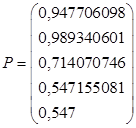
При этом эффект распространения, вызванный дополнительным ростом заработной платы в легкой промышленности на 5% (считая, что доли заработной платы в добавленной стоимости по отраслям соответственно равны 0,5, 0,517, 0,499, 0,345, 0,547) дается мультипликатором эффекта распространения

.

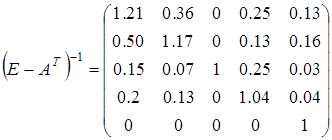Задание 2

Условие задания:

Имеются данные экономического развития США за 1953 - 1974 гг

 Скачать реферат