Метод потенциалов для решения транспортной задачи в матричной форме. Задача оптимального распределения ресурсов

Рефераты / Экономико-математическое моделирование / Метод потенциалов для решения транспортной задачи в матричной форме. Задача оптимального распределения ресурсов

Получаем матрицу мнений экспертов размерностью N·n, в которой сумма элементов любого столбца равна

Наиболее подготовленного кандидата из группы на основе коллективной оценки выбирают после расчета среднего ранга для каждого из кандидатов:

,

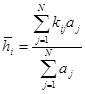На первом

месте будет кандидат, имеющий минимальный ранг, что будет соответствовать усредненному мнению коллектива из N экспертов.

Если мнения экспертов сильно расходятся, то необходимо ввести процент достоверности, т.е. согласованности экспертов. Согласованность экспертов определяется степенью рассеянности средних рангов .

Степень рассеяния определяется с помощью дисперсии средних рангов:

,

;

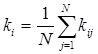М(k) – математическое ожидание среднего ранга.

В таблице для краткости обозначений принято:

Таблица 1 - Расчет коэффициента согласованности

Номер члена группы

Оценка эксперта

0

1

2

3

4

5

6

7

8

9

1

4

3

4

4

2

5

4

1

3

7

3,72

3,70

0,09

2

7

7

5

7

1

6

7

7

4

5

5,59

5,60

2,56

3

5

4

3

3

5

3

3

3

7

2

3,78

3,80

0,04

4

3

6

7

6

3

7

6

6

6

3

5,21

5,30

1,69

5

6

1

2

1

4

2

2

2

1

4

2,63

2,50

2,25

6

2

3

6

5

6

4

5

5

5

1

4,06

4,20

0,04

7

1

2

1

2

7

1

1

4

2

6

2,81

2,70

1,69

Уровень компетентности аi

0,9

0,8

0,7

0,6

0,8

0,9

0,6

0,9

0,7

0,9

7,8

 

8,36

При полном совпадении мнений экспертов дисперсия имеет максимальное значение:

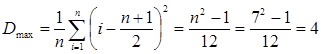
Критерий согласованности экспертов представляется в виде отношения:

,

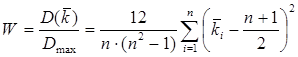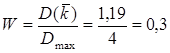
Ответ: Выбран кандидат №5, имеющий минимальный ранг.

Мнение экспертов согласовано не очень хорошо (лишь на 30%).

Скачать реферат Скачать реферат
Страница:  1  2  3  4  5  6  7  8  9 


Другие рефераты на тему «Экономико-математическое моделирование»:

Поиск рефератов

Последние рефераты раздела

Copyright © 2010-2024 - www.refsru.com - рефераты, курсовые и дипломные работы