Суммирование расходящихся рядов

Рефераты / Математика / Суммирование расходящихся рядов

Непосредственно ясно, что рассматриваемый метод “обобщенного суммирования” является линейным. Что же касается регулярности этого метода, то она устанавливается следующей теоремой принадлежащей Абелю.

2.2 Теорема Абеля [1]

Теорема. Если ряд (А) сходится и имеет сумму А (в обычном смысле), то для сходи

тся степенной ряд (1), и его сумма стремится к пределу А, когда .

Доказательство. Начнем с того, что радиус сходимости ряда (1) не меньше 1, так что для ряд (1), действительно, сходится. Мы имели уже тождество

(где ); вычтем его почленно из тождества

Полагая , Придем к тождеству

(4)

Так как то по произвольно заданному найдется такой номер , что , лишь только .

Разобьем сумму ряда в правой части (4) на две суммы

Вторая оценивается сразу и независимо от :

Что же касается первой, то она стремится к 0 при и при достаточной близости к 1 будет

так что окончательно 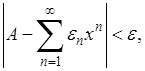что и доказывает утверждение.

Если ряд (А) суммируем по Пуассону-Абелю к сумме А, то в обычном смысле, как мы видели, он может и не иметь суммы. Иными словами из существования предела

, (5)

вообще говоря, не вытекает сходимость ряда (А). Естественно возникает вопрос, какие дополнительные условия надлежит наложить на поведение членов этого ряда, чтобы из (5) можно было заключить о сходимости ряда (), т.е. о существовании для него суммы в обычном смысле. Первая теорема в этом направлении была доказана Таубером.

2.3 Теорема Таубера

Теорема. Пусть ряд (1) сходится при 0<x<1, и имеет место предельное равенство (5). Если члены ряда (А) таковы, что

(6)

то и

Доказательство. Разобьем доказательство на две части. Сначала

предположим, что Если положить то при величина , монотонно убывая, стремится к нулю.

Имеем при любом натуральном N

так что:

Взяв произвольно малое число , положим

Так что при . Пусть теперь выбрано достаточно большим чтобы: выполнялось неравенство ; соответствующее x было настолько близко к 1, что

. Тогда

Что и доказывает утверждение теоремы.

К рассмотренному частному случаю теоремы приводится и общий. Положим

так что

и затем

(7)

Но из предположения теоремы, т.е. из того, что при , легко получить, что

. (8)

Для доказательства этого достаточно разбить здесь сумму на две:

и выбрать N таким, чтобы во второй сумме все множители были по абсолютной величине меньшими наперед заданного числа , тогда и вторая сумма по абсолютной величине будет меньше , каково бы ни было х; относительно первой суммы, состоящей из определенного конечного числа слагаемых, того же можно достигнуть за счет приближения х к 1.