Расчет вихревого холодильно-нагревательного аппарата

Рис.2.1 – 1 – Зависимость адиабатного КПД схемы от суммарной доли

охлажденного потока при

2 – Зависимость адиабатного КПД схемы от суммарной доли

охлажденного потока при

3 –За

висимость адиабатного КПД схемы от суммарной доли охлажденного потока при

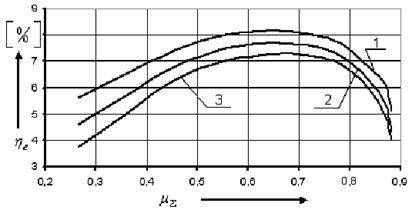
Рис.2.2 – 1 – Зависимость эксергетического КПД от суммарной доли охлажденного потока при

2 – Зависимость эксергетического КПД от суммарной доли охлажденного потока при

3 – Зависимость эксергетического КПД от суммарной доли охлажденного потока при

Рис.2.3 – 1 – Зависимость термического КПД от суммарной доли охлажденного потока

2 – Зависимость термического КПД от суммарной доли

охлажденного потока при

3 – Зависимость термического КПД от суммарной доли

охлажденного потока при

3 Расчет потребного количества сжатого воздуха

Расчетная холодопроизводительность схемы

,

где - потребная холодопроизводительность. По техническому заданию , - потери тепла через изоляцию стенок термокамеры

, ,

где - поверхность теплообмена ;

- внутренняя поверхность термокамеры.

Потребный объем термокамеры

Толщина изоляции: .

Внешняя поверхность камеры: .

Расчетная поверхность теплообмена: .

Изоляция: пенопласт марки Ф-Ф.

Коэффициент теплопроводности изоляции:

Расчет холодного воздуха для охлаждения стенок термокамеры

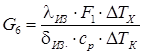
4 Расчет эжектора.

Эжектор 6

Исходные данные:

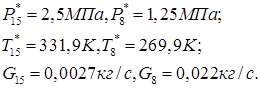
Где - давление, температура и расход эжектирующего (активного) газа;

- давление, температура и расход эжектируемого (пассивного) газа;

Статическое давление на выходе из эжектора принимаем равным

1- сопло эжектирующего газа

2- сопло эжектируемого газа

3- камера смешения

4- диффузор

Рис. 4.1 – Расчетная схема эжектора

Считая ср=const определяем коэффициент эжекции

.

Определяем безразмерные параметры:

Область реально возможных режимов. Найдем критическую величину - предельно возможное значение , при котором в сечении запирания скорость эжектируемого газа, то есть . Так как отношение - невелико, то воспользуемся уравнением, полученным в предположении равенства статических давлений в сечении запирания:

Откуда следует при

Определяем из уравнения

Подставляя численные значения, получим =0,987.

Этому значению соответствует предельно возможное значение λ2=0,90.

Из уравнения импульсов, которое принимает вид

,

Определим значение , то есть при или

Таким образом, предельно возможное значение оказывается выше, чем определено из рассмотрения потоков сечении запирания (λ2=0,90).

Принимаем .

Для расчета эжектора зададимся рядом значений коэффициента скорости λ2 . Задаемся несколькими значениями и проводим расчет по изложенному выше методу.

Данные расчета и результаты заносим в таблицу 2.4.

Таблица 2.4

 Скачать реферат