Электричество и магнетизм, изучение свойств ферромагнетиков

(6.5)

Коэффициент Холла или постоянная Холла определяется из условия равенства сил:

(6.6)

Из (6.6) следует, что

, (6.7)

где - подвижность носителей заряда.

В соответствии с (6.5), напряженность поля Холла можно определить в виде:

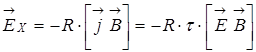. (6.8)

Сопоставляя (6.7) и (6.8) видим, что

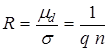, (6.9)

где n - концентрация носителей заряда в единице объема. Из (6.9) следует, что постоянная Холла обратно пропорциональна концентрации носителей заряда и ее знак совпадает со знаком носителей заряда. Поле Холла (6.8) приводит к появлению э. д. с. Холла Vx, которая с учетом выражения (6.9) и геометрических размеров имеет вид:

, (6.10)

где - ток через датчик.

В реальном кристалле полупроводника носители рассеиваются на примесях и колебаниях решетки. Учет данных процессов для полупроводников с собственной а) и примесной б) проводимостью приводит к следующему выражению для R:

а) 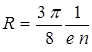, б) 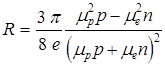, (6.11)

где e - заряд электрона, , - подвижности электронов и дырок, n и p - их концентрации. Знак постоянной Холла позволяет определить тип преимущественной проводимости полупроводника.

Методика эксперимента

Установка содержит механическую систему перемещения датчика Холла вдоль оси соленоида с фиксацией его положения, блок питания БП-1 соленоида, стрелочный прибор для регистрации тока соленоида и электронную схему измерения тока датчика Холла и холловскую э. д. с. (Рис.6.2). При определении э. д. с. Холла следует учесть сопутствующие эффекту Холла гальваномагнитные, термомагнитный и другие эффекты, которые являются четными по полю, то есть не зависят от направления вектора индукции B. Данное обстоятельство используется для их исключения - холловскую э. д. с. измеряют при двух направлениях магнитного поля, изменяя его направление переключателем П1.

Рис.6.2

При прямом направлении поля B+ напряжение между холловскими контактами , при обратном , что после вычитания дает:

, (6.12)

то есть Vдоб, обусловленное четными эффектами исключено.

Из формулы (6.10) следует, что зависимость э. д. с. Холла от индукции магнитного поля Vx (B) имеет линейный характер. Поэтому тангенс угла наклона прямой к оси абсцисс, вдоль которой ориентирована индукция поля, определим в следующем виде:

(6.13)

Равенство (6.13) позволяет вычислить постоянную Холла:

(6.14)

В реальных кристаллах постоянная Холла зависит от концентрации по закону, определяемому соотношением (6.11а), из которого можно определить с учетом (6.14) концентрацию носителей заряда в единице объема:

. (6.15)

В положении переключателя "ПРОВ" определяется удельное электрическое сопротивление кристалла датчика r по измеренному падению напряжения V к величине тока i:

(6.16)

Так как плотность тока , где m - подвижность носителей тока и , то

(6.17)

Порядок выполнения работы

Эксперимент осуществляется в следующей последовательности. В положении переключателя П1 - "0" и П2 - "ПРОВОД" снять зависимость тока через датчик Холла от разности потенциалов. Изменение напряжения осуществляется потенциометром R. Переключатель "П2" перевести в положение "Vx". Потенциометром R задать ток через датчик и измерить э. д. с. Холла при изменении магнитного поля соленоида в прямом и обратном направлении. Изменение знака поля осуществляется переключателем "Н - 0-Н+". Для этого датчик поместить в любую точку на оси соленоида (обычно в центре), для которой известна зависимость индукции поля от тока через соленоид, регулируемого потенциометром Rc.Э. д. с. Холла найти в результате двух измерений по формуле (6.12). Измерения повторяются несколько раз при других значениях тока через датчик Холла. Далее снять распределение поля по оси соленоида в положении переключателя П2 - "Vx".

Обработка результатов эксперимента

1. Определение удельного сопротивления датчика.

Построить зависимость разности потенциалов V от тока i через датчик Холла по экспериментальным точкам по методу наименьших квадратов:

, (6.18), где , (6.19)

in и Vn - измеренные значения тока и разности потенциалов в положении переключателя П1 - "0", N - число измерений. Удельное сопротивление датчика r определяется по формуле:

(6.20)

2. Расчеты постоянной Холла R, концентрации n и подвижности m.

Построить линейную зависимость (градуировочная прямая) по экспериментальным точкам по методу наименьших квадратов:

, (6.21)

где A и С определяются по формулам

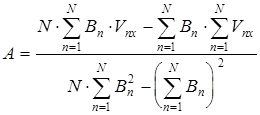
, (6.22)

Постоянную Холла R, концентрацию n и подвижность m определяем из выражений (6.14), (6.15) и (6.17):

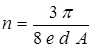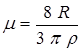; ; (6.23)

При расчетах использовать заданную градуировочную кривую индукции поля соленоида от тока через него.

3. Определить значения э. д. с. Холла Vx, соответствующие различным координатам датчика x при его перемещении вдоль оси соленоида. Используя градуировочную прямую п.2, определить значения Вх в указанных положениях датчика и построить зависимость Вх от координаты

 Скачать реферат