Электричество и магнетизм, изучение свойств ферромагнетиков

(3.10)

Индуктивность катушки, заполненной магнетиком с магнитной проницаемостью, рассчитывается по формулам:

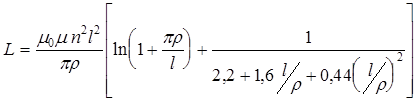(3.11)

(3.12)

3. Определим величину переменного тока в цепи, состоящей из

катушки индуктивности с активным сопротивлением , подключенной к источнику переменного напряжения .

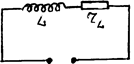
Рис.3.3

В соответствии с формулами (4.11) и (4.12) этот ток изменяется по закону

(3.13)

Амплитуда тока и фаза определяются амплитудой, параметрами цепи , и частотой w:

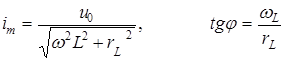(3.14)

Из (3.14) следует, что ток в цепи отстает по фазе от приложенного напряжения на угол , который зависит от параметров цепи и частоты:

, (3.15), где

- полное электрическое сопротивление цепи.

Зависимость амплитуды тока от выражает закон Ома для цепи переменного тока. Если w=0, то по цепи течет постоянный ток, для которого

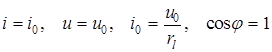(3.16)

Методика эксперимента

Экспериментальная установка состоит из двух источников постоянного и переменного токов: регулировка которых осуществляется потенциометром . Измерения токов и осуществляется амперметром .

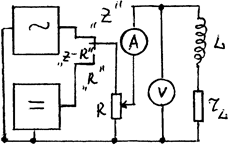
Рис.3.4

Вольтметр измеряет напряжение на катушке индуктивности.

В установке предусмотрены элементы, позволяющие измерять одним и тем же прибором характеристики переменного и постоянного тока.

Порядок выполнения работы

1. В положении переключателя "" осуществить проверку закона Ома для цепи постоянного тока. При различных положениях ручки потенциометра зарегистрировать ток и напряжение на активном сопротивлении катушки.

2. Снять зависимость тока в цепи переменного тока от напряжения на катушке в положении "" переключателя.

3. Аналогичные измерения в п.2 провести для катушки со стальным сердечником, который ввинчивается в катушку индуктивности на правой панели прибора.

Обработка результатов эксперимента

1. На основании результатов измерений определить величину активного сопротивления , используя метод наименьших квадратов для линеаризации функции :

, (3.17), где 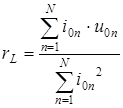(3.18)

где N - число измерений и .

2. Используя метод наименьших квадратов, аналогичным образом определить :

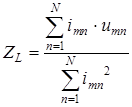(3.19)

3. Вычислить индуктивность катушки без сердечника:

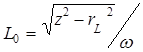(3.20)

4. Вычисления п. п.1-3 повторить для катушки с сердечником и найти .

5. Определить магнитную проницаемость сердечника, используя формулу:

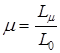(3.21)

6. Рассчитать индуктивность катушки по формуле (3.11), используя известные геометрические размеры соленоида. Сравнить теоретические и экспериментальные результаты.

Расчет погрешностей

1. Расчет погрешности определения активного сопротивления катушки.

Вычисление активного сопротивления катушки rL и случайной составляющей по имеющейся зависимости Напряжения U от тока I осуществляется с помощью метода наименьших квадратов. При этом уравнение линейной регрессии имеет вид , где A - угловой коэффициент наклона прямой, проходящей через начало координат. Этот коэффициент находиться по формуле (II.8), где xi=Ii, yi=Ui, A=rL.

Погрешность определения углового коэффициента DA находится из соотношения (II.9).

Здесь необходимо также учесть приборные погрешности определения активного сопротивления по формуле:

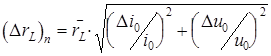
где - класс точности амперметра, - класс точности вольтметра.

Суммирование случайной и систематической погрешности осуществляется по формуле (II.10):

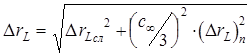
2. Расчет погрешности определения полного сопротивления катушки.

Вычисление z и по имеющейся зависимости амплитудного значения напряжения Um от амплитудного значения силы тока Im в цепи осуществляется аналогично тому, как это делалось в случае постоянного тока, с помощью метода наименьших квадратов по формулам (II.8), (II.9), где xi=Imi, yi=Umi, A=Z. Учет приборной погрешности

позволяет определить полную погрешность, что дает:

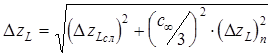
3. Определение индуктивности и погрешности индуктивности катушки.

 Скачать реферат