Электричество и магнетизм, изучение свойств ферромагнетиков

Формула для определения индуктивности:

Абсолютная погрешность определяется как погрешность косвенного измерения, что дает:

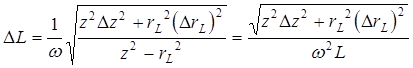
Вопросы для самопроверки

Определите зависимость

индукции магнитного поля в произвольной точке пространства от тока, протекающего по проводнику.

В чем заключаются отличия э. д. с. индукции от э. д. с. самоиндукции?

Как зависит э. д. с. самоиндукции от геометрических размеров контура с током?

Вычислите индуктивность бесконечного соленоида.

Как определяется полное сопротивление индуктивности при переменном токе?

Получите формулу для определения индукции магнитного поля в коротком соленоиде.

В каком порядке производятся теоретические и экспериментальные исследования?

Лабораторная работа 3.

RLC - КОНТУР

Цель работы: изучение электромагнитных колебаний в последовательном RLC - контуре; исследование затухающих колебаний; снятие резонансных кривых; определение добротности полосы пропускания, резонансной частоты и декремента затухания; сравнение теоретических и экспериментальных кривых.

ОСНОВНЫЕ ПОНЯТИЯ

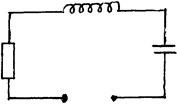
Рис.4.1

Конденсатор C, катушка индуктивности L и активное сопротивление R, соединенные последовательно, образуют колебательный RLC - контур. Электрические колебания в контуре возбуждаются в результате периодического обмена между энергией электрического поля конденсатора 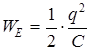и энергией магнитного поля катушки индуктивности , где q и C - заряд и емкость конденсатора, 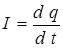- ток в контуре, L - индуктивность катушки. В результате протекания тока в контуре на активном сопротивлении R выделяется тепловая энергия, приводящая к потере энергии электрических колебаний. Заряд, сосредоточенный на обкладках конденсатора в начальный момент времени t0=0, уменьшается с течением времени и создает ток в контуре, изменяющийся во времени. Величину тока, протекающего в цепи при разряде, можно определить из закона Ома для неоднородного участка контура:

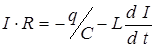(4.1)

Сила тока равна скорости изменения заряда, так что (4.1) эквивалентно дифференциальному уравнению второго порядка

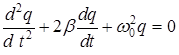, (4.2)

где введены обозначения: ,

Решение уравнения (4.2) представим в виде линейной комбинации

, (4.3)

l1, l2 - корни характеристического уравнения .

Из приведенной зависимости следует, что при выполнении неравенства , заряд быстро затухает во времени и колебания в контуре отсутствуют. Такой процесс называется апериодическим. Колебания в контуре существуют только при выполнении условия . Применяя формулу Эйлера для комплексных величин, заменим выражение (4.3) на сумму гармонических функций:

(4.4)

где , - собственная частота затухающих колебаний в контуре. Заряд q принимает только вещественное значение, так что величины A и B могут быть только сопряженными комплексными числами. Результирующую зависимость заряда от времени t можно определить в виде:

, (4.5)

где q0 и j - произвольные постоянные, имеющие смысл амплитуды колебаний в момент времени t=0, j - начальная фаза.

Отношение 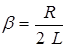характеризует быстроту уменьшения амплитуды колебаний и называется коэффициентом затухания. При b=0 уравнение (4.2) описывает незатухающие колебания в контуре, причем определяет частоту собственных колебаний. Графики зависимости заряда от времени при различных значениях коэффициента затухания, представлены на рис.4.2

а) , б) , в)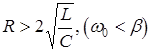

Рис.4.2

В соответствии с видом функции (4.5), изменение заряда во времени можно рассматривать как гармоническое колебание частоты w1 с амплитудой, изменяющейся по закону . Отношение амплитуд в моменты времени, отличающиеся друг от друга на величину периода T, называется декрементом затухания, а его логарифм - логарифмическим декрементом затухания и обозначается символом l:

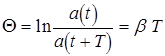(4.6)

Логарифмический декремент затухания характеризует колебательную систему и имеет определенный физический смысл. За время t, в течение которого амплитуды a (t) уменьшается в e раз, система совершает колебаний. Из условия следует, что , так что логарифмический декремент затухания обратно пропорционален числу колебаний, совершаемых за время, в течение которого амплитуда уменьшается в e раз.

Для характеристики колебательной системы часто используют величину

, (4.7)

которую называют добротностью колебательной системы.

Периодическая во времени внешняя э. д. с., включенная в последовательный контур, создает в нем вынужденные колебания.

Суммируя напряжение с э.д.с. самоиндукции, получаем из (4.1) уравнение для определения заряда:

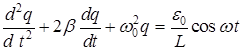(4.8)

Общее решение уравнения (4.8) равно сумме общего решения однородного уравнения при e0=0 и частного решения неоднородного уравнения. Общее решение однородного уравнения определяется формулой (4.5) и затухает с ростом времени. Частное решение уравнения (4.8) найдем методом комплексных амплитуд. В соответствии с данным методом, представим уравнение в виде реальной части комплексного уравнения

 Скачать реферат