Эконометрическая модель национальной экономики Германии

.

Вычислим также выровненные значения Ĉ и Î. (Приложение 2)

На втором шаге запишем уравнения в стандартном виде, т.е. по одной эндогенной переменной в левой части с коэффициентом 1. Эндогенные же переменные в правых частях заменим на их выровненные значения.

Рассмотрим второй шаг применительно к первому у

равнению, для этого в него вместо подставим , тогда получим

или

Т.к. согласно первоначальной модели , последнее уравнение запишется как модель парной регрессии

,

в которой зависимой переменной служит , а независимой – .

МНК-оценки параметров этой модели имеют вид

.

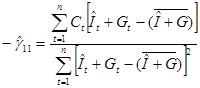
Подставив в последние формулы значения временных рядов , и получим

.

.

Подставляя эти значения в формулы, имеем:

.

.

Таким образом, применение двухшагового МНК к первому уравнению структурной формы позволило идентифицировать первое уравнение первоначальной формы: .

Рассмотрим второй шаг для второго уравнения, для этого в него вместо подставим , тогда получим:

Или

.

Поскольку , то последнее уравнение запишется как модель парной регрессии:

,

в которой зависимой переменной служит , а регрессором выступает – (), поэтому МНК – оценки параметров этой модели имеют вид:

Подставив в последние формулы значения временных рядов , получим:

Подставляя эти значения в формулы:

.

.

Таким образом, применение двухшагового МНК ко второму уравнению структурной формы позволило идентифицировать второе уравнение первоначальной формы: .

Найдем оценки дисперсий случайных составляющих , .

Для этого решим систему уравнений, подставив в левую часть квадрат стандартной ошибки для регрессий потребления по государственным расходам, а также чистых инвестиций по государственным расходам:

Таким образом, по итогам двухшагового МНК эконометрическая модель имеет вид:

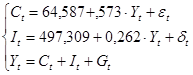
3. Построение прогноза эндогенных переменных модели на 2008, 2009 гг.

Для прогноза эндогенных переменных на шагов вперед (в нашем случае на два шага) необходимо задать значения предопределенных переменных Предопределенная переменная в нашей работе (в нашем случае экзогенная) – (государственные расходы в год ). Поскольку у нас нет данных о будущих государственных расходах, то получим их путем прогноза по линейному тренду: .

Оценки параметров линейного тренда получаем как МНК-оценки параметров парной регрессии:

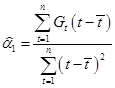
Используя пакет прикладных программ Excel, получим оценки коэффициентов линейного тренда:

 Скачать реферат