Определение зависимости цены товара

Задача состоит в построении линейной модели зависимости цены колготок от их плотности, состава и фирмы-производителя в торговых точках города Москвы и Московской области весной 2006 года.

Цена колготок – это зависимая переменная Y. В качестве независимых, объясняющих переменных были выбраны: плотность (DEN) X1, содержание полиамида X2 и лайкры X3, фирма-производитель X4.

Описание пере

менных содержится в Таблице 1.1:

Таблица 1.1.

Задание:

1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции. Поясните выбор факторов для включения в модель.

2. Постройте уравнение регрессии. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверьте с помощью F-критерия; оцените качество уравнения регрессии с помощью коэффициента детерминации .

3. Постройте уравнение множественной регрессии только со статистически значимыми факторами. Рассчитайте доверительный интервал для каждого наблюдения (уровень значимости примите равным 5%). Результаты п.3 отобразить графически (исходные данные,

Решение.

1.Для проведения корреляционного анализа необходимо выполнить следующие действия:

Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.

Выбрать команду Сервис – Анализ данных.

В диалоговом окне анализ данных выберите инструмент Корреляция, а затем щелкнуть на кнопке ОК.

В диалогом окне Корреляция в поле Входной интервал необходимо ввести диапазон ячеек, содержащих исходные данные(значения Х и У).Если выделены и заголовки столбцов, то установить флажок Метки в первой строке.

Выбрать параметры вывода. ОК.

Матрица парных коэффициентов корреляции.

Анализ матрицы коэффициентов парной корреляции показывает, что фактор Х3(содержание лайкры) оказывает наибольшее влияние на У(цена колготок), т.к.

КПК │rx2x3=-0.67│ ‌< 0.8

значит, мультиколлинеарность отсутствует.

Посмотрим как влияют коэффициенты Х2 и Х3 на У.

│ ryx2= -0.56 │ < │ryx3=0.6│,

следовательно фактор Х3 оказывает большее влияние на У, но в ММР включаем и Х2 и Х3, т.к. Явление МК отсутствует.

2.Для проведения регрессионного анализа выполним:

Команду Сервис – Анализ данных. В диалоговом окне выберем инструмент Регрессия, а затем ОК. В поле Входной интервал У введем адрес значений У из заданной таблицы. В поле Входной интервал Х – адрес значений Х.

Данные регрессионного анализа:

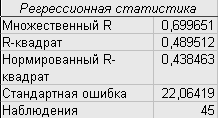
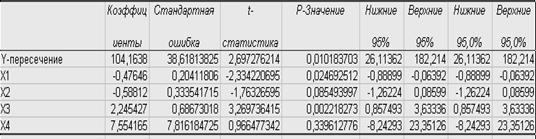
Запишем модель регрессии в линейной форме:

У=104,16 – 0,48Х1 – 0,59Х2 + 2,25Х3 + 7,55Х4

Оценим значимость факторов с помощью Т –критерия Стьюдента, для этого, определим его табличное значение при уровне значимости 0,05.

к =n-m-1=45-4-1=40 t-кр.таб=2.0211

Сравним расчетные значения с табличным по модулю:

│t X1= -2.334│ > t –табл. = 2,021,

следовательно фактор Х1(плотность) является статистически значимым, и статистически значимым признается влияние плотности колготок на их цену.

│t X2= -1,763│< t –табл. = 2,021,

следовательно фактор Х2 – содержание полиамида – является статистически незначимым.

│t X3= 3,269 │> t –табл. = 2,021,

следовательно фактор Х3 – содержание лайкры – является статистически значимым, и статистически значимым признается влияние содержания лайкры в колготках на их цену.

│t X4= 0,966 │< t –табл. = 2,021,

следовательно фактор Х4 – фирма-производитель – является статистически незначимым.

Оценка статистической значимости уравнения регрессии в целом осуществляется по F – критерию Фишера: Fтабл.= 2,61

Так как Fрасч. > Fтабл.(9,59 > 2.61), то уравнение регрессии можно признать статистически значимым (адекватным).

Оценка общего качества уравнения регрессии происходит с использованием коэффициента детерминации.

Так как R=0.489, то 48,9% вариации результативного показателя – цены колготок – объясняется вариацией факторных признаков, включенных в модель регрессии – плотность, содержание лайкры и полиамида, фирмы – производителя.

3.Постройте уравнение множественной регрессии только со статистически значимыми факторами. Рассчитайте доверительный интервал для каждого наблюдения, (уровень значимости примите равным 5%). Укажите торговые точки, в которых цены завышены.

 Скачать реферат