Особенности термического режима рек

Форма верхней части эпюры зависит от многих факторов, влияющих на теплообмен на границе «река-атмосфера». Типы 1,4,7 соответствуют охлаждению водной массы за счет теплообмена с атмосферой. На реках такие формы эпюры формируются в период суточного, синоптического или сезонного охлаждения водной массы. Типы эпюр 2,5,8 в естественных условиях формируются в период суточного, синоптического или сезо

нного нагревания водной массы. Типы эпюр 3,6,9 возникают в том случае, если тепловое взаимодействие атмосферы и речной водной массы уравновешено. Они могут формироваться в утренние и вечерние часы, когда интенсивность солнечной радиации компенсируется эффективным излучением воды. Кроме того, нередко формирование такой формы эпюры у берегов при малых глубинах и малых скоростях течения. При очень больших скоростях течения происходит практически полное смешивание различных слоев водной массы, поэтому в любую погоду, независимо от сезона, эпюра температур выражена слабо.

Основные типы эпюр температуры хорошо соответствуют реальному распределению температуры у поверхности и у дна водных потоков. Для р. Невы, например, наименее изменчивой по форме частью эпюры оказалась придонная зона водного потока. Наоборот, температура воды в поверхностном слое отличается максимальной изменчивостью (рис. 4.22). В этом слое наблюдается изменение θ во времени, абсолютной величины градиента температуры по глубине. С началом дневного нагревания водной массы (с 7:00) тип эпюры температур постепенно изменяется с типа 7 на 8.

Температура воды в каждой точке вертикали (в соответствии с формулой (3.17)) изменяется в зависимости от характерных температур , , глубины потока и коэффициента шероховатости русла (), параметра а1. При использовании этой формулы для описания распределения температуры воды на вертикали оказалось, что если считать а1=427, то изменение температуры воды по вертикали равно нулю. Соответствие с фактическими эпюрами достигается при а1=0,06–0,2.

Изменение глубины потока h и шероховатости n относительно слабо влияют на изменение относительного распределения температуры воды. Например, при увеличении глубины потока с 1 м до 10 м (прочие условия равны, θ1=200С, θп=20,30С) изменение температуры на глубине 0,1h составило -0,0005% (уменьшилось на 0,0120С), на глубине 0,2h изменение температуры равно -0,0002% (уменьшилось на 0,0040С). При дальнейшем увеличении относительной глубины различия температуры становятся еще менее заметными.

При расчетах изменения температуры воды по вертикали с использованием формулы (3.17), увеличение коэффициента шероховатости с 0,02 (соответствует ровным незаросшим руслам) до 0,04, что соответствует поймам, поросшим кустарником, ведет к уменьшению градиентов температуры в верхнем слое водной массы на 0,2% и к увеличению температуры в средней и нижних частях эпюры на 0,01–0,020С. При увеличении коэффициента шероховатости до 0,1, что соответствует густо облесенным поймам (Маккавеев, Чалов, 1986) увеличение градиента в верхней части эпюры составляет 0,03%, а в средней части эпюры разница температуры для этих двух случаев составляет 0,01–0,050С. Это относительно большие изменения, так как общий перепад температуры воды на вертикали составляет 0,130С (соответствует максимальному значению Δθэ, по измерениям на р. Ока). Глубина вертикали не имеет большого значения для формирования эпюры температур. Наоборот значение коэффициента шероховатости является значимым фактором в формировании температурной эпюры.

Данные наблюдений свидетельствуют о возможной связи распределения температуры воды по глубине со средней скоростью на вертикали. Для проверки этой гипотезы, заменим в уравнении (3.10) скорость в данной точке, осредненную по времени, на среднюю скорость на вертикали. В этом случае при подстановке в уравнение выражения получим:

(4.1)

С учетом замечаний о знаке «минус» в степени при экспоненте:

(4.2)

Анализ уравнения (4.2) показывает, что если принять распределение скоростей на вертикали по уравнению эллипсоида (Караушев, 1969), то изменение поверхностной скорости потока не влияет на распределение температуры по глубине, поскольку:

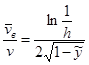. (4.3)

Отношение скоростей не зависит от величины скорости, а является функцией глубины потока и расстояния до дна. Аналогичный по смыслу результат получается при использовании параболического закона распределения местной скорости по глубине:

(4.4)

Сравнение результатов, полученных по формулам (3.17) и (4.2) при разных способах аналитического описания скоростной эпюры, коэффициентах шероховатости, величинах =23,260С, =23,390С, характеризует табл. 4.4. Значения , соответствуют данным наблюдений на р. Ока в 2007 г. при наибольшей изменчивости температуры на вертикали. Из анализа этой таблицы следует, что различия в значениях температуры воды, рассчитанных по разным формулам (θф2 – θф1 и θф3 - θф1), на всех горизонтах не превышают 0,010С при любых значениях коэффициента шероховатости n. Следовательно, учет отношения скоростей выражением (4.1) не дает преимуществ по сравнению с расчетным распределением температуры по вертикали формулой (3.17). Кроме того, скорость потока косвенно учитывается при расчете Сш для вычисления параметра М по формуле, предложенной в работе. Увеличение этого параметра приводит, согласно формуле Шези-Маннинга, к уменьшению скорости потока, и выравниванию температуры воды на вертикали.

Для проверки эффективности формулы (3.17) необходимо заранее исключить те из измеренных температурных эпюр, которые не могут соответствовать формуле в силу особенностей ее теоретического обоснования. При выводе формулы считалось, что изменение температуры по ширине потока незначительно по сравнению с изменением по глубине потока. Это условие обеспечило устранение членов уравнения теплопроводности описывающих изменение температуры в поперечном сечении. Например, при проверке эффективности формулы (3.17) нельзя использовать измерения в зоне смешения потока. Как показала практика, критерием отбора вертикалей для этой цели является величина Δθэ < 0,10С.

Попытки сравнивать данные наблюдений и результаты расчета привели к необходимости более точно задавать относительную глубину каждой точки измерений. При расчете коэффициента при втором члене уравнения (3.17) учитывается поверхностная температура воды. Поэтому для более точного расчета поверхностную температуру воды необходимо рассчитывать. Это легко сделать, выразив величину через формулу (3.17) и считая величину отрицательной величиной:

 Скачать реферат