Синтез системы угловой стабилизации дозвукового транспортного самолета по заданному курсу

Из графика видно, что при значении коэффициента Кос=0.1 запас по фазе составляет φ=40.9˚. Из этого следует, что данная система устойчива.

График переходного процесса в замкнутом рулевом приводе с жесткой обратной связью имеет вид при значении коэффициентов Ку=100 и Кос=0.1:

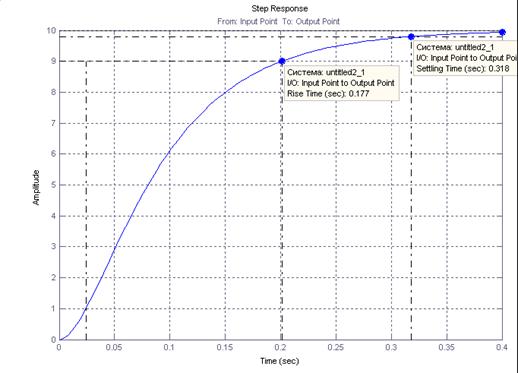
Рис. >7. Переходный процесс в рулевом приводе

Из графика рис. 7 видно, что время переходный процес в замкнутом рулевом приводе с жесткой обратной связью при значении коэффициентов Ку=1, Кос=0.1 имеет следующие параметры:

Время переходного процесса – 0.318 сек.

Время нарастания – 0.177 сек.

Установившееся величина – 10 град.

Составим структурную схему разомкнутой системы управления автопилотом и определим значение коэффициентов Кп, К1 .

Структурная схема разомкнутой системы управления автопилотом имеет вид:

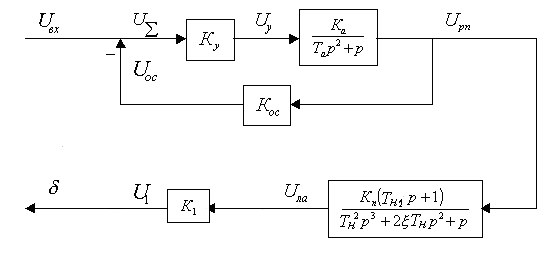
Рис. 8. Структурная схема разомкнутой системы управления автопилотом

Для определения коэффициентов Кп, К1 смоделируем структурную схему разомкнутой системы управления автопилотом в программной среде MathLab 6.5 (рис 9).

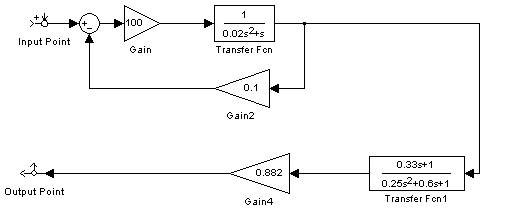
Рис. 9. Структурная схема разомкнутой системы управления автопилотом в среде MathLab 6.5

Приведем ЛАФЧХ разомкнутой системы управления автопилотом:

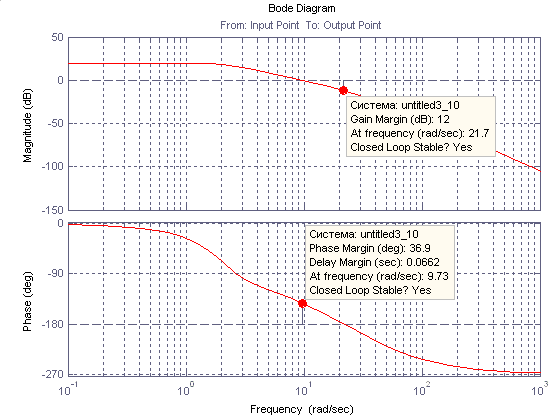
Рис. 10. ЛАФЧХ разомкнутой системы управления автопилотом

Приняв Кп=1 и построив графики ЛАФЧХ разомкнутой системы управления автопилотом (рис. 10), можно сказать, что при значении коэффициента, К1=0.882, запас по фазе составляет Δφ=36,9˚, а запас по амплитуде ΔL =12Дб. Из этого следует, что данная система устойчива.

Составим структурную схему замкнутой системы по отношению к внешнему управляющему моменту и построим ЛАФЧХ и график переходного процесса этой системы.

Структурная схема замкнутой системы по отношению к внешнему управляющему моменту показана на рис 11.

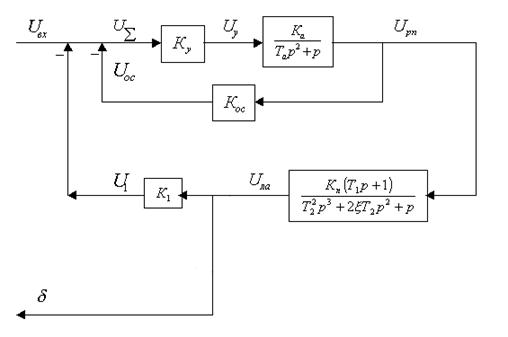
Рис. 11. Структурная схема замкнутой системы управления автопилотомпо отношению к внешнему управляющему моменту

Согласно техническому заданию коэффициент по управляющему моменту равен 1. С учетом этого построим ЛАФЧХ и график переходного процесса этой системы. Смоделируем структурную схему замкнутой системы по отношению к внешнему управляющему моменту в программной среде MathLab 6.5 (рис. 12).

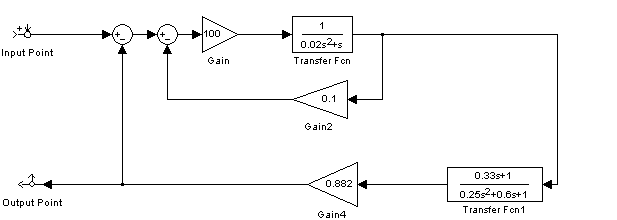
Рис. 12. Структурная схема замкнутой системы управления автопилотомпо отношению к внешнему управляющему моменту ОС в среде MathLab 6.5

На рис. 13 показана ЛАФЧХ замкнутой системы по отношению к внешнему управляющему моменту.

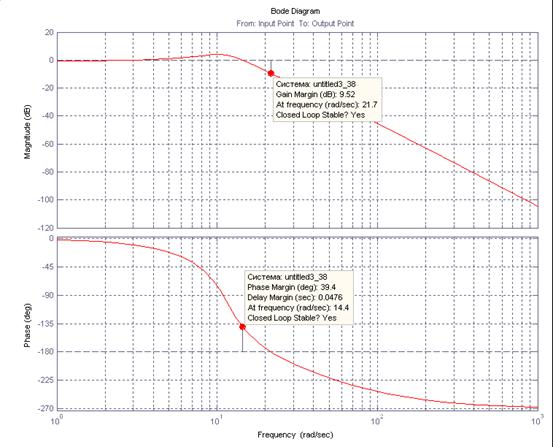
Рис. 13. замкнутой системы по отношению к внешнему управляющему моменту

График переходного процесса замкнутой системы как реакции на единичное управляющее воздействие показан на рис. 14.

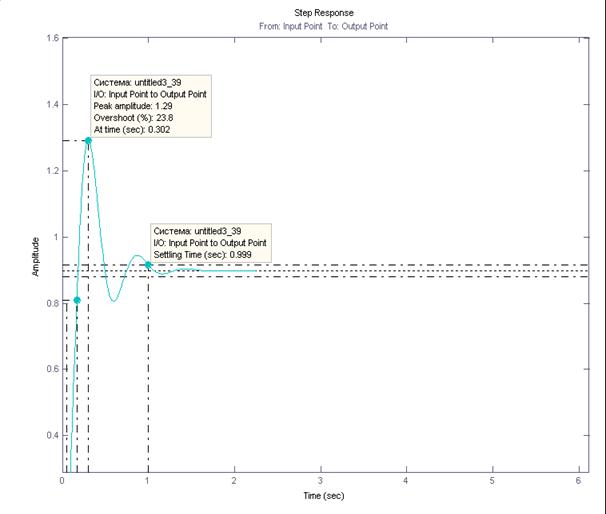
Рис. 14. Переходный процес замкнутой системы на единичное управляющее воздействие

Из графика видно, что время переходного процесса как реакции на единичное управляющее воздействие при соответствующих коэффициентах составляет примерно 1с, Перерегулирование составляет 23,8%. Время нарастания 1 сек. Максимальная величина равна 1,29 град.

Составим структурную схему замкнутой системы по отношению к внешнему возмущающему моменту и построим ЛАФЧХ и график переходного процесса этой системы.

Структурная схема замкнутой системы по отношению к внешнему возмущающему моменту показана на рис 15.

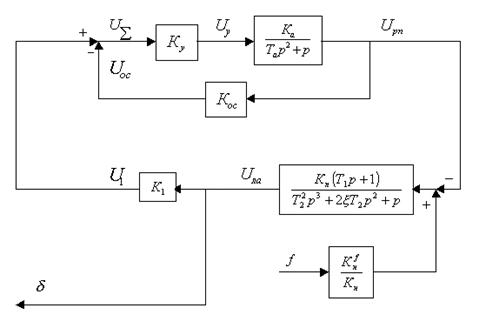
Рис. 15. Структурная схема замкнутой системы по отношению к внешнему возмущающему моменту

Для построения ЛАФЧХ и графика переходного процесса этой системы смоделируем структурную схему замкнутой по отношению к внешнему возмущающему моменту в программной среде MathLab 6.5 (рис. 16).

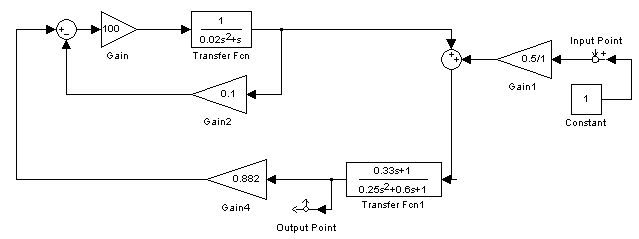
Рис. 16. Замкнутая схема ЛА-АП по отношению к внешнему возмущающему моменту в программной среде MathLab 6.5

Приведем ЛАФЧХ замкнутой системы по отношению к внешнему возмущающему моменту:

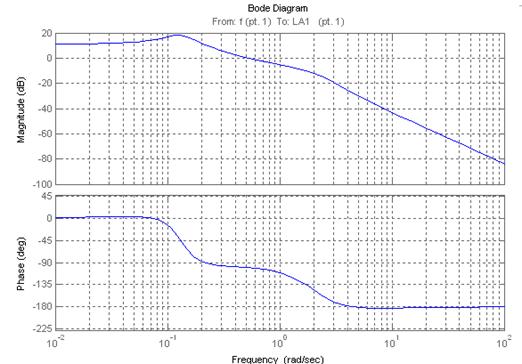
Рис. 17. ЛАФЧХ замкнутой системы ЛА-АП по отношению к внешнему возмущающему моменту

График переходного процесса замкнутой системы как реакции на единичное возмущающее воздействие имеет вид:

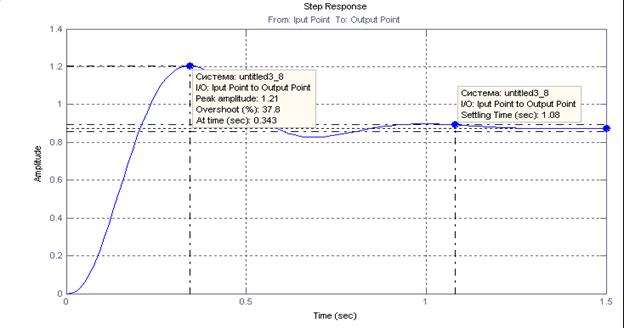
Рис. 18. Переходный процесса замкнутой системы ЛА-АП на единичное возмущающее воздействие

Из графика видно, что переходный процесс замкнутой системы ЛА-АП по возмущающему воздействию при соответствующих выбранных коэффициентах имеет следующие параметры:

Время переходного процесса – 1,08 сек.

Время нарастания – 0,343 сек.

Установившееся величина – 0,875 град.

Вывод

В процессе выполнения работы по синтезу системы угловой стабилизации дозвукового транспортного самолета по заданному курсу была составлена схема сил и моментов, действующих на объект, составлена система уравнений «система угловой стабилизации - транспортный самолет», линеаризована эта система, составлены структурные схемы и получены передаточные функции разомкнутой и замкнутой системы. Методом ЛАФЧХ исследована устойчивость объекта, определено значение общего коэффициента усиления по контуру при котором система имеет необходимые запасы устойчивости по амплитуде и фазе. Построена ЛАФЧХ разомкнутой системы. Построена ЛАФЧХ замкнутой системы по отношению к внешнему возмущающему моменту. Построена ЛАФЧХ замкнутой системы по отношению к управляющему моменту. Построены графики переходных процессов, как реакции на единичное управляющее и возмущающее воздействие.

На основе полученных результатов и анализа построенных ЛАФЧХ и графиков переходных процессов системы угловой стабилизации дозвукового транспортного самолета по заданному курсу можно сказать, что при подобранных значениях коэффициентов система устойчива, имеет хороший запас по фазе и небольшое время переходных процессов.

Список использованной литературы

1. Боднер В.А. Системы управления летательными аппаратами. – М.: Машиностроение, 1973. 504с.

2. Кузовков Н.Т. Системы стабилизации летательных аппаратов.-М.:Высшая школа,1976.304с.

3. Павлов В.А., Понырко Е.А., Хованский Ю.М. Стабилизация летательных аппаратов и автопилоты.-М.: Высш.шк., 1964.483 с.

 Скачать реферат

Страница:  1  2  3  4 

Другие рефераты на тему «Транспорт»:

• Сущность и параметры рабочего процесса поршневого двигателя внутреннего сгорания
• Транспортная логистика
• Автомобильные датчики и интеллектуальные транспортные системы
• Контроль и регулирование движения судна
• Перевозки грузов железнодорожным видом транспорта