Параметры и силы, влияющие на вагон при движении
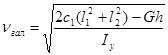 (5)
(5)
где l1 +l2 = L – база вагона;
h – высота центра тяжести вагона с грузом над уровнем рессорного подвешивания
Iy – момент инерции вагона с грузом относительно оси, проходящей в плоскости верха рессор и направленной перпендикулярно оси пути.

Тогда
![]() (6)
(6)
Из формулы 7 следует, что чем меньше жесткость рессорного подвешивания с1, чем больше момент инерции кузова Iy и выше центр тяжести h, тем меньше частота собственных колебаний галопирования nгал и тем больше период галопирования Tгал.
Колебания боковой качки могут быть рассмотрены с помощью той же схемы, приняв в ней вместо l1 и l2 величины b1 и b2 и вместо момента инерции кузова вагона Iy (относительно оси y) – момент инерции кузова вагона относительно оси x – Ix
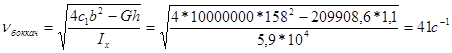
Тогда период колебаний будет равен
![]()
Линейные частоты колебаний кузова определяются по формуле:
![]()
Тогда
![]()
![]()
![]()
Следовательно, чем больше величина частоты, тем больше плавность хода вагона.
2. Расчет параметров гасителей колебаний
Задан гаситель с постоянной силой трения
![]()
где Nтр – нормальная сила (нажатие) в трущейся паре гасителя;
j - коэффициент трения частей пары.
3. Проверка рессорного подвешивания на отсутствие «валкости»
Для определения высоты метоцентра рассмотрим вагон, вес кузова которого G и жесткость рессоры с. Тогда, реакции рессорных комплектов при наклоне кузова на угол q составят:

Момент реакции рессор относительно точки О1
![]()
Заменим действие силы R1 и R2 их равнодействующей R, а точку пересечения равнодействующей в наклонной осью вагона назовем метацентром вагона. Момент равнодействующей R относительно точки O1
![]()
где hМ – высота метацентра от пола вагона.
Поскольку угол q мал, то tgq»0, т.е. M0=RhMq, где R = R1 + R2 = Q, то приравнивая момент силы R1 и R2 моменту от их равнодействующей R, получим qhMG = 2b2ecq, отсюда
![]()
где fст – статический прогиб рессорного подвешивания вагона;
b – половина базы тележки.
![]()
Высота метацентра выше центра тяжести вагона более чем на 2 м, следовательно вагон устойчив.
4. Составление дифференциального уравнения вынужденных колебаний подпрыгивания вагона и нахождение аналитического выражения описывающего процесс вынужденных колебаний подпрыгивания вагона
Решение дифференциального уравнения n = 2p/Т является аналитическим выражением процесса вынужденных колебаний подпрыгивания вагона при движении его по регулярным неровностям вида z = hcoswt.
Это решение имеет вид:
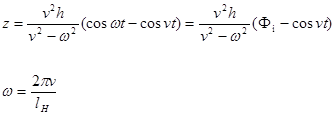
где n - скорость движения вагона;
lн – длинна периода неровностей;
2h – высота неровностей;
n - круговая частота собственных колебаний
Для колеса вагона номер i возмущение функции имеет вид:
![]()
где li – расстояние от первого до i-го колеса.
Амплитуда вынужденных колебаний подпрыгивания кузова вагона будет иметь вид:
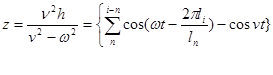
Для заданного вагона
![]()
Аналитическое выражение описывающее процесс вынужденных колебаний будет иметь вид:
![]()
Для построения графика определяем зависимость z от t
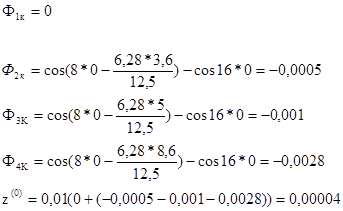
При t=1 сек

Для других значений t
![]()
ЧАСТЬ II
1. Расчет динамических боковых и рамных сил при вписывании вагона в кривых участках пути
Наибольшие боковые силы возникают тогда, когда при движении вагона наибольшее допустимое непогашенное ускорение на вагон достигает 0,7 м/с2. Это возможно при минимально допустимом для этой кривой возвышении наружного рельса. Его можно определить используя формулу:

Величина действующей на одну тележку поперечной горизонтальной силы:
![]()
где m – масса вагона;
анет – непогашенное поперечное ускорение;
Hв – сила ветра, действующая на вагон и направленная поперек пути
![]()
Принимая aнет = 0,8 м/с2, получим
![]()
При действии на вагон продольных сил S, которые могут возникнуть, например при рекуперативном напряжении на шкворень тележки действуют дополнительная сила Hторм которая приближенно равна:
![]()
Наибольший угол y можно определить по формуле:
![]()
Общее усилие на шкворень в этом случае
![]()
где S – продольное усилие в поезде;
2k – расстояние между клиновыми отверстиями автосцепок.
![]()
Поскольку, в своем движении по кривой тележка непрерывно вращается вокруг полюса поворота, то образующийся от силы H0брт момент относительно точки О уравновешивается направляющим усилием Y (давление гребня набегающего колеса первой оси тележки на боковую поверхность) поперечными силами трения колес по рельсам.
![]()
где P – вертикальная нагрузка, передаваемая колесом рельсу;
m - коэффициент трения колесом по рельсу (принимаем m = 0,25).
Уравнение проекций этих сил имеет вид:
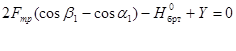
Другие рефераты на тему «Транспорт»:
Поиск рефератов
Последние рефераты раздела
- Проект пассажирского вагонного депо с разработкой контрольного пункта автосцепки
- Проектирование автомобильных дорог
- Проектирование автотранспортного предприятия МАЗ
- Производственно-техническая база предприятий автомобильного транспорта
- Расчет подъемного механизма самосвала
- Системы автоблокировки
- Совершенствование организации движения и снижение аварийности общественного транспорта в городе Витебск
