Математическое моделирование пластической деформации кристаллов

Программа позволяет проводить как обычную МД, так и использовать процедуру минимизации. Программа позволяет исследовать влияние ориентации кристалла, скорости деформирования и температуры на процесс деформирования. Она также позволяет использовать свободные и периодические граничные условия на боковых, относительно растяжения, сторонах кристалла.

С помощью программы проведено моделировани

е пластического деформирования двумерных кристаллов с гексагональной решеткой. Такие решетки характерны для базисной плоскости ГПУ кристаллов и для плоскости (111) ГЦК кристаллов. Начальная температура 0.025. На рис.3 приведена сумма полной энергия кристалла и произведенной над ним работы (на один атом кристалла) как функция времени. Видно, что с точностью до 5 знака эта величина сохраняется, что свидетельствует о правильности работы программы.

Рис.3 Зависимость сумма полной энергия кристалла и произведенной над ним работы (на один атом кристалла) как функция времени.

На рис.4 приведено напряжение, поперечное относительно направления растяжения, как функция времени. Видно, что оно почти все время поддерживается невысоким. Это свидетельствует о правильности выбранного алгоритма регулирования ширины ячейки моделирования.

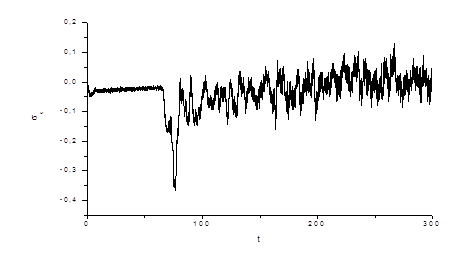
Рис.4 Зависимость напряжения, поперечного относительно направления растяжения, от времени.

Наконец, на рис.5 приведена кривая напряжение-деформация. Эта кривая полностью соответствует экспериментальным кривым напряжение-деформация для совершенных кристаллов.

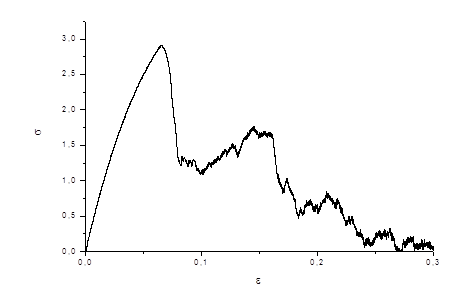
Рис.5 Кривая растяжения совершенного кристалла

На этой кривой можно выделить несколько стадий в деформировании кристалла [18,19]. На первой, упругой стадии, происходит накопление энергии. Затем, по мере роста напряжения кристалл переходит в нелинейную область, в конце которой появляются дислокации. Начинается сброс напряжения, который заканчивается появлением полос скольжения, которые и обеспечивают дальнейший сброс напряжения. Затем происходит частичное упрочнение кристалла с последующими сбросами напряжения. На этой стадии происходит накопление вакансий, их слияние в вакансионные поры. На последней стадии поры, объединяясь, дают начало трещине, которая, развиваясь, разрывает кристалл. На рис.6-11 даны изображения кристалла, которые иллюстрируют описанную выше стадийность пластического деформирования и разрушения кристалла.

Заключение

1. Изучен метод молекулярной динамики со всеми его важнейшими ингредиентами: потенциал взаимодействия, граничные условия, алгоритм интегрирования по времени, задание начальных условий, контроль термодинамических параметров в процессе моделирования, контроль достижения термодинамического равновесия, измерение физических величин. Изучены особенности применения метода молекулярной динамики к исследованию пластичности реакторных материалов.

2. Создана программа для изучения пластичности в кристаллах. Создана программа визуализации процесса пластической деформации и разрушения кристаллов. Предложен новый подход к моделированию растяжения кристаллов, близкий к используемому в эксперименте. Предложено динамическое уравнение для поперечного размера ячейки моделирования.

3. Проведено моделирование развития пластической деформации ГПУ кристаллов при одноосном растяжении. Показана принципиальная возможность имитации с помощью этого метода кривых растяжения совершенных кристаллов, изменения температуры образца, появления дислокаций, полос скольжения, одиночных вакансий и их скоплений, а также процесса разрушения кристаллов.

Список использованных источников

1. В.В.Кирсанов, ЭВМ-эксперимент в атомном материаловедении, Энергоатомиздат, 1990.

2. J.Schiotz, Scripta Mater., 51, 837 (2004).

3. K.W.Jacobsen, J.K.Norskov, M.J.Puska, Phys. Rev. B35, 7423 (1987).

4. K.W.Jacobsen, P.Stoltze, J.K.Norskov, Surf. Sci. 366, 394 (1996).

5. L.Verlet, Phys. Rev. 159, 98 (1967); Phys. Rev. 165, 201 (1967).

6. D. van der Spoel, E. Lindahl, B. Hess at al. Gromacs User Manual, v. 3.2, University of Groningen.

7. K. Refson. Moldy User’s Manual, v. 2.16, (2001).

8. W.Smith, M.Leslie, T.R.Forester. The DL_POLY_2 User Manual, (2003), Daresbery Laboratory.

9. J.B.Gibson, A.N.Goland, M.Milgram, G.H.Vineyard, Phys. Rev. 120, 1229 (1960).

10. M.P.Allen, D.J.Tildesley Computer simulation of liquids. Clarendon Press, Oxford, 1989.

11. K.Nordlund, Comput. Mater. Sci., 3, 448 (1995).

12. J.F.Ziegler, J.P.Biersack, U.Littmark, The stopping and range of ions in solids. Pergamon Press, N.Y., 1987.

13. J.Schiotz, T.Vegge, F. D. Di Tolla, K.W.Jacobsen, Phys. Rev. B60, 11971 (1999),cond-mat/9902165.

14. T.Egami, K.Maede, and V.Vitek, Phil. Mag. A 41, 883 (1980).

15. J.R.Ray and A.Rahman, J. Chem. Phys. 80, 4423 (1984).

16. H.Jonsson and H.C.Andersen, Phys. Rev. Lett. 60, 2295 (1988).

17. A.S. Clarke and H.Jonsson, Phys. Rev. E 47, 3975 (1993).

18. Р.Хоникомб Р. Пластическая деформация металлов. М. Мир. 1972.

19. И.М.Неклюдов, Н.В.Камышанченко. Физические основы прочности и пластичности металлов. ч. 3. Пластическая деформация и разрушение кристаллических материалов. Изд. “Педагогика-Пресс” и Белгородского государственного университета, Белгород, 2001

 Скачать реферат