Математическое моделирование пластической деформации кристаллов
1.2. Потенциал
Для моделирования материала необходимо задать потенциал взаимодействия составляющих его атомов. Наиболее простым является парный потенциал Леннарда-Джонса
|
|
(2) |
Здесь, ![]() - расстояние между атомами,
- расстояние между атомами, ![]() - глубина потенциальной ямы и
- глубина потенциальной ямы и ![]() связано с положением минимума потенциала
связано с положением минимума потенциала ![]() . Потенциал Леннарда-Джонса качественно правильно описывает взаимодействие между атомами – сильное отталкивание на малых расстояниях, обусловленное первым слагаемым в скобках, и притяжение на больших расстояниях, за которое отвечает второе слагаемое в скобках. Он хорошо описывает ван-дер-ваальсовское взаимодействие между атомами кристаллов благородных газов, но, вследствие своей простоты, часто используется для качественного описания взаимодействия других атомов. С потенциалом Леннарда-Джонса проведено большое количество вычислений. Он является стандартным в вычислениях методом МД.
. Потенциал Леннарда-Джонса качественно правильно описывает взаимодействие между атомами – сильное отталкивание на малых расстояниях, обусловленное первым слагаемым в скобках, и притяжение на больших расстояниях, за которое отвечает второе слагаемое в скобках. Он хорошо описывает ван-дер-ваальсовское взаимодействие между атомами кристаллов благородных газов, но, вследствие своей простоты, часто используется для качественного описания взаимодействия других атомов. С потенциалом Леннарда-Джонса проведено большое количество вычислений. Он является стандартным в вычислениях методом МД.
Основными материалами реакторостроения являются металлы – сталь, цирконий и т.д. В металлах природа сил взаимодействия между атомами не двухчастичная (парная) а многочастичная. Effective Medium Theory (EMT) дает реалистическое описание металлической связи с учетом её многочастичной природы [3,4]. EMT- потенциал, с вычислительной точки зрения, не намного сложнее парного потенциала, но дает намного более реалистическое описание свойств материалов. Поскольку в данной работе не ставится задача изучения пластических свойств конкретного материала мы будем использовать модельный потенциал Леннарда-Джонса.
Удобно при этом выбрать в качестве единицы длины ![]() , единицы энергии
, единицы энергии ![]() и единицы массы - массу атомов
и единицы массы - массу атомов ![]() (полагаем, что материал состоит из атомов одного сорта). Это приводит к ускорению вычислений. Чтобы перейти к величинам, характеризующим конкретный материал, необходимо ввести соответствующие масштабные множители -
(полагаем, что материал состоит из атомов одного сорта). Это приводит к ускорению вычислений. Чтобы перейти к величинам, характеризующим конкретный материал, необходимо ввести соответствующие масштабные множители - ![]() для длины,
для длины, ![]() для времени,
для времени, ![]() для скорости,
для скорости, ![]() для силы,
для силы, ![]() (
(![]() в двумерном случае) для напряжения, где
в двумерном случае) для напряжения, где ![]() и
и ![]() взяты для данного материала.
взяты для данного материала.
Потенциал Леннарда-Джонса простирается до бесконечности. Однако на больших расстояниях он мал. И поэтому его влияние на движение далеких атомов мало. Чтобы ускорить вычисления эту несущественную часть потенциала отбрасывают, или, другими словами, вводят обрезание потенциала
|
|
(3) |
Радиус обрезания ![]() традиционно выбирают
традиционно выбирают ![]() или
или ![]() . Возможные причины такого выбора будут обсуждаться ниже. В данной работе будет использоваться радиус обрезания
. Возможные причины такого выбора будут обсуждаться ниже. В данной работе будет использоваться радиус обрезания ![]() . Другие необходимые изменения в потенциале Леннарда-Джонса будут обсуждаться в разделе, посвященном выполнению закона сохранения энергии в МД.
. Другие необходимые изменения в потенциале Леннарда-Джонса будут обсуждаться в разделе, посвященном выполнению закона сохранения энергии в МД.
1.3. Алгоритм интегрирования по времени
Основным компонентом программ, использующих метод молекулярной динамики, является алгоритм интегрирования по времени. Он необходим, чтобы проинтегрировать уравнения движения взаимодействующих частиц и найти их траектории.
Алгоритм интегрирования по времени основывается на методе конечных разностей, время при этом задается на конечной сетке, шаг по времени есть расстояние между последовательными точками сетки. Зная положения и скорости в момент времени ![]() (точные детали зависят от типа алгоритма) схема интегрирования дает те же величины в более поздний момент времени
(точные детали зависят от типа алгоритма) схема интегрирования дает те же величины в более поздний момент времени ![]() . Используя процедуру интегрирования временную эволюцию системы можно прослеживать в течении длительного времени.
. Используя процедуру интегрирования временную эволюцию системы можно прослеживать в течении длительного времени.
Конечно, эти схемы приближенными, и, поэтому, существуют ошибки, связанные с ними. Они классифицируются так:
Ошибки обрывания, связанные с точностью метода конечных разностей по отношению к истинному решению. Метод конечных разностей обычно базируется на ряде Тейлора, оборванном на некотором члене. Эти ошибки не зависят от программной реализации метода, они присущи самому алгоритму.
Ошибки округления, связаны с ошибками, возникающими при программной реализации алгоритма. Например, такие ошибки возникают из-за конечного числа цифр, используемых в компьютерной арифметике.
Оба типа ошибок можно уменьшить, уменьшая ![]() . Для больших
. Для больших ![]() ошибки обрывания доминируют, но они быстро уменьшаются, когда
ошибки обрывания доминируют, но они быстро уменьшаются, когда ![]() уменьшается. Например, алгоритм Верле имеет ошибки обрывания пропорциональные
уменьшается. Например, алгоритм Верле имеет ошибки обрывания пропорциональные ![]() для каждого временного шага интегрирования. Ошибки округления падают более медленно с уменьшением
для каждого временного шага интегрирования. Ошибки округления падают более медленно с уменьшением ![]() и доминируют в пределе малых
и доминируют в пределе малых ![]() . Использование 64-битной точности (соответствующую “двойной точности” в Fortrane) помогает сохранить ошибки округления минимальными.
. Использование 64-битной точности (соответствующую “двойной точности” в Fortrane) помогает сохранить ошибки округления минимальными.
В молекулярной динамике наиболее часто используемым алгоритмом интегрирования по времени является, вероятно, так называемый алгоритм Верле [5]. Основная идея состоит в том, чтобы записать разложение Тейлора до третьего порядка вперед и назад по времени. Пусть ![]() обозначает скорость,
обозначает скорость, ![]() - ускорение и
- ускорение и ![]() - третью производную от
- третью производную от ![]() по
по ![]() . Тогда имеем:
. Тогда имеем:
|
|
(4) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

 ,
, 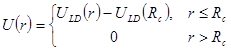 .
.