Математическое моделирование пластической деформации кристаллов
Оба типа ошибок можно уменьшить, уменьшая шаг интегрирования по времени, что, однако, увеличивает время вычислений.
Другой тип ошибок возникает из-за использования потенциала с обрезанием. Скачок потенциала на радиусе обрезания при пластической деформации, когда атомы могут двигаться друг относительно друга, приводит к значительному нарушению закона сохранении энергии. Использование потенци
ала без скачка (3) позволяет существенно улучшить выполнения закона сохранения энергии. Потенциал (3), однако, имеет скачок производной (силы) на радиусе обрезания ![]() . Это также приводит к несоблюдению закона сохранения энергии. Оно особенно ярко проявляется при уменьшении радиуса обрезания от канонических значений
. Это также приводит к несоблюдению закона сохранения энергии. Оно особенно ярко проявляется при уменьшении радиуса обрезания от канонических значений ![]() и
и ![]() . Это связанно с тем, что канонические значения радиуса обрезания находятся в минимумах радиального распределения атомов гексагональной решетки. Когда же
. Это связанно с тем, что канонические значения радиуса обрезания находятся в минимумах радиального распределения атомов гексагональной решетки. Когда же ![]() попадает в максимум радиального распределения число атомов, то испытывающих действие силы (при
попадает в максимум радиального распределения число атомов, то испытывающих действие силы (при ![]() ), то прекращающих испытывать ее действие (при
), то прекращающих испытывать ее действие (при ![]() ), становиться очень большим, что и приводит к существенному несохранению энергии. Чтобы избавиться от скачка производной потенциала на радиусе обрезания
), становиться очень большим, что и приводит к существенному несохранению энергии. Чтобы избавиться от скачка производной потенциала на радиусе обрезания ![]() потенциал был модернизирован. Пусть
потенциал был модернизирован. Пусть
|
|
(14) |
где
|
|
(15) |
и ![]() ,
, ![]() ,
, ![]() . Тогда модернизированный потенциал имеет вид
. Тогда модернизированный потенциал имеет вид
|
|
(16) |
Модернизированный потенциал гладко сшивается (до второй производной) с потенциалом Леннарда-Джонса на радиусе сшивки ![]() и зануляется вместе со своей первой производной на радиусе обрезания
и зануляется вместе со своей первой производной на радиусе обрезания ![]() . С этим потенциалом при значениях параметров
. С этим потенциалом при значениях параметров ![]() и
и ![]() были проведены все расчеты в данной работе.
были проведены все расчеты в данной работе.
1.12. Вычисление физических величин
При деформировании системы все физические величины, такие как напряжение ![]() , температура
, температура ![]() , кинетическая энергия
, кинетическая энергия ![]() , потенциальная энергия
, потенциальная энергия ![]() характеризующие деформируемую систему меняются. Их мгновенные значения, усредненные по малым промежуткам времени чтобы исключить тепловые колебания, описывают состояние деформируемой системы. В отличие от равновесных систем мы не можем теперь использовать усреднение по времени, а должны использовать усреднение по различным начальным состояниям системы.
характеризующие деформируемую систему меняются. Их мгновенные значения, усредненные по малым промежуткам времени чтобы исключить тепловые колебания, описывают состояние деформируемой системы. В отличие от равновесных систем мы не можем теперь использовать усреднение по времени, а должны использовать усреднение по различным начальным состояниям системы.
Кинетическая и потенциальная энергия находятся как
|
|
(17) | |
|
|
(18) |
Температура определяется как
|
|
(19) |
где ![]() - размерность системы. В двухмерном случае
- размерность системы. В двухмерном случае ![]() - средней кинетической энергией. Выражение для тензора напряжений, основанное на вириальной теореме [14,15], имеет вид
- средней кинетической энергией. Выражение для тензора напряжений, основанное на вириальной теореме [14,15], имеет вид
|
|
(20) |
где ![]() -
- ![]() -компоненты тензора напряжений для атома
-компоненты тензора напряжений для атома ![]() ,
, ![]() - объем, приходящийся на атом
- объем, приходящийся на атом ![]() (
(![]() , где
, где ![]() - полный объем системы),
- полный объем системы), ![]() - масса атома
- масса атома ![]() ,
, ![]() -
- ![]() -компонента его импульса,
-компонента его импульса, ![]() - расстояние между атомами
- расстояние между атомами ![]() и
и ![]() (
(![]() - компонента вектора, направленного от
- компонента вектора, направленного от ![]() -го атома к
-го атома к ![]() -му атому). Это выражение для тензора напряжений не единственное, существуют и другие его определения. Однако, когда напряжения усредняются по объему различные определения быстро сходятся к макроскопическому полю напряжений. Во время моделирования кривые напряжение - деформация строятся после усреднения атомного напряжения по всей системе.
-му атому). Это выражение для тензора напряжений не единственное, существуют и другие его определения. Однако, когда напряжения усредняются по объему различные определения быстро сходятся к макроскопическому полю напряжений. Во время моделирования кривые напряжение - деформация строятся после усреднения атомного напряжения по всей системе.
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

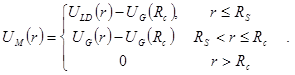
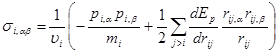 ,
,