Математическая постановка краевых задач уравнения теплопроводности

Коэффициент конвективной теплоотдачи αк зависит:

1) от формы и размеров поверхности, отдающей тепло (шар, цилиндр, пластина) и от ее положения в пространстве (вертикального, горизонтального, наклонного);

2) от физических свойств теплоотдающей поверхности;

3) от свойств окружающей среды (ее плотности, теплопроводности и вязкости, в свою очередь зависящих от температуры), а также

4) от разности температур Тs - Тс.

В этом случае в соотношении

qs = α·[Тs(τ) - Тс], (3.10)

коэффициент α будет суммарным коэффициентом теплообмена:

α = αк+ α(Т) (3.11)

В дальнейшем нестационарный теплообмен тела, механизм которого описывается соотношением (3.10), будем называть теплообменом по закону Ньютона.

По закону сохранения энергии количество тепла qs(τ), отданного поверхностью тела, равно количеству тепла, которое подводится изнутри к поверхности тела в единицу времени к единице площади поверхности путем теплопроводности, т. е.

qs(τ) = α·[Тs(τ) - Тс(τ)] = -λ(∂T/∂n)s (3.12)

где для общности постановки задачи температура Тс считается переменной, а коэффициент теплообмена α(Т) приближенно принят постоянным [α(Т) = α= const].

Обычно граничное условие пишут так:

λ(∂T/∂n)s + α·[Тs(τ) - Тс(τ)] = 0 (3.13)

Из граничного условия третьего рода, как частный случай, можно получить граничное условие первого рода. Если отношение α/λ стремится к бесконечности [коэффициент теплообмена имеет большое значение (α→∞) или коэффициент теплопроводности мал (λ→ 0)], то

Тs(τ) - Тс(τ) = lim [1/(α∕λ)·(∂T/∂n)s] = 0

α∕λ→∞

откуда

Тs(τ) = Тс(τ)

т. е. температура поверхности теплоотдающего тела равна температуре окружающей среды.

Аналогично при α→0 из (x) получаем частный случай граничного условия второго рода — адиабатическое условие (равенство нулю потока тепла через поверхность тела). Адиабатическое условие представляет другой предельный случай условия теплообмена на границе, когда при весьма малом коэффициенте теплоотдачи и значительном коэффициенте теплопроводности поток тепла через граничную поверхность приближается к нулю. Поверхность металлического изделия, соприкасающегося со спокойным воздухом, при недолгом процессе может приниматься адиабатической, так как действительный поток теплообмена через поверхность незначителен. При длительном процессе поверхностный теплообмен успевает отнять у металла значительное количество тепла, и пренебрегать им уже нельзя.

4. Граничное условие четвертого рода соответствует теплообмену поверхности тела с окружающей средой [конвективный теплообмен тела с жидкостью) или теплообмену соприкасающихся твердых тел, когда температура соприкасающихся поверхностей одинакова. При обтекании твердого тела потоком жидкости (или газа) передача тепла от жидкости (газа) к поверхности тела в непосредственной близости к поверхности тела (ламинарный пограничный слой или ламинарный подслой) происходит по закону теплопроводности (молекулярный перенос тепла), т. е. имеет место теплообмен, соответствующий граничному условию четвертого рода

Тs(τ) = [Тс(τ)]s (3.14)

Помимо равенства температур, имеет место также равенство потоков тепла

-λc(∂Tc/∂n)s = -λ(∂T/∂n)s (3.15)

Дадим графическую интерпретацию четырех видов граничных условий (рис. 3.1).

Скалярная величина вектора теплового потока пропорциональна абсолютной величине градиента температуры, который численно равен тангенсу угла наклона касательной к кривой распределения температуры вдоль нормали к изотермической поверхности, т.е

(∂T/∂n)s = tg φs

На рис. 3.1 изображены на поверхности тела четыре элемента поверхности ∆S с нормалью к ней n (нормаль считается положительной, если она направлена наружу). По оси ординат отложена температура.

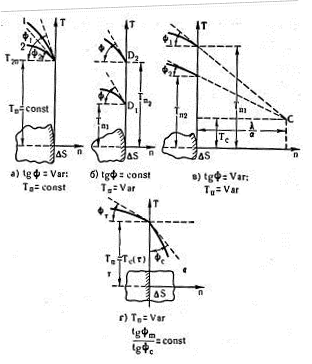
Рис. 3.1 Различные способы задания условий на поверхности

Граничное условие первого рода состоит в том, что задана Тs (τ); в простейшем случае Тs (τ) = const. Отыскивается наклон касательной к температурной кривой у поверхности тела, а тем самым и количество тепла, отдаваемое поверхностью (см. рис. 3.1., а).

Задачи с граничными условиями второго рода имеют обратный характер; задается тангенс угла наклона касательной к температурной кривой у поверхности тела (см. рис. 3.1, б); находится температура поверхности тела.

В задачах с граничными условиями третьего рода температура поверхности тела и тангенс угла наклона касательной к температурной кривой—величины переменные, но задается на внешней нормали точка С, через которую должны проходить все касательные к температурной кривой (см. рис. 3.1, в). Из граничного условия (3.13) следует

tg φs = (∂T/∂n)s = (Тs(τ) - Тс)/(λ∕α) (3.16)

Тангенс угла наклона касательной к температурной кривой у поверхности тела равен отношению противолежащего катета [Тs(τ)—Тc]

к прилежащему катету λ∕α соответствующего прямоугольного треугольника. Прилежащий катет λ∕α является величиной постоянной, а противолежащий катет [Тs (τ) — Тс] непрерывно изменяется в процессе теплообмена прямо пропорционально tg φs. Отсюда следует, что направляющая точка С остается неизменной.

В задачах с граничными условиями четвертого рода задается отношение тангенсов угла наклона касательных к температурным кривым в теле и в среде на границах их раздела (см. рис. 3.1, г):

tg φs /tg φc = λc∕λ = const (3.17)

с учетом совершенного теплового контакта (касательные у поверхности раздела проходят через одну и ту же точку).

Выбирая для расчета тип того или иного простейшего граничного условия, следует помнить, что в действительности поверхность твердого тела всегда обменивается теплом с жидкой или газообразной средой. Можно приближенно считать границу тела изотермической в тех случаях, когда интенсивность поверхностного теплообмена заведомо велика, и адиабатической – если эта интенсивность заведомо мала.

 Скачать реферат