Коллоидная химия

,

где - удельный поток диффузии, характеризующий количество вещества, переносимое за единицу времени через единицу площади.

,

Принимая отсюда , т.е. коэффициент диффузии численно равен количеству вещества, про диффундировавшего через единицу площади в единицу времени.

,

Это уравнение Эйнштейна. Для частиц, по форме близких к сферическим, .

,

где - масса 1 моля вещества.

Так как существует связь между броуновским движением и диффузией, то должна существовать связь между средним квадратичным значением проекции смещения частицы и коэффициентом диффузии . Эта связь была установлена Эйнштейном (1905г.) и независимо от него Смолуховским (1906 г.):

,

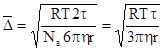Пользуясь уравнением Эйнштейна-Смолуховского и, зная и всех величин, можно вычислить число Авогадро.

Теория броуновского движения, созданная Эйнштейном и Смолуховским, подтвердила реальное существование молекул. Исследование броуновского движения привело к созданию теории флуктуации и способствовало развитию статической физики.

Флуктуации представляют собой спонтанные отклонения какого-нибудь параметра от среднего равновесного значения в достаточно малых объемах системы. Флуктуация представляет собой явление как бы обратное явлению диффузии.

4. Гипсометрический закон Лапласа

Уравнение Лапласа носит название гипсометрического закона.

,

Этот закон был экспериментально подтвержден Перреном (1910г.). Изучая распределение монодисперсной суспензии гуммигута, он использовал уравнение Лапласа для определения числа Авогадро, которое оказалось равным 6,82*1023 (точное значение 6,024*1023). Гипсометрический закон соблюдается и в аэрозолях, частицы которых имеют небольшую плотность и размер не более 0,05мкм.

Этому закону подчиняется распределение газа по высоте:

,

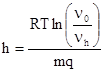С помощью этой формулы удобно вычислять для любой свободнодисперсной системы величину , представляющую собой высоту, на которую надо подняться, чтобы численная концентрация уменьшилась с до .

5 Кинетическая или седиментационная устойчивость коллоидно-дисперсных систем. Седиментационый анализ. Вывод уравнения радиуса частиц. Кривые распределения. Монодисперсность и полидисперсность. Методы седиментационного анализа (в поле земного тяготения, в поле центробежной силы – центрифугирование). Их практическое значение

Способность дисперсной системы сохранять равномерное распределение частиц по всему объему принято называть седиментационной, или кинетической устойчивостью системы.

Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения частиц с помощью соответствующих уравнений рассчитывают размеры частиц.

Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность.

Размер частицы дисперсной фазы обычно характеризуют радиусом частицы, реже объемом или площадью ее поверхности. Радиус однозначно определяется только для частиц сферической формы.

В монодисперсной системе все частицы осаждаются с одинаковой скоростью. В соответствии с этим такую же скорость перемещения имеет граница осветления, концентрация частиц по уменьшающейся высоте столба суспензии сохраняется постоянной и также с постоянной скоростью увеличивается масса осевших частиц. Если - общая масса дисперсной фазы, - первоначальная высота столба суспензии, то - масса дисперсной фазы в объеме, приходящаяся на единицу высоты столба суспензии. При скорости осаждения частиц в течение времени вещество осядет из столба высотой , и масса осевшего вещества составит

, (1)

Это уравнение описывает кинетику седиментации в монодисперсной системе. Если принять, что частицы имеют сферическую форму и при их осаждении соблюдается закон Стокса, то, используя формулу:

, (2)

получим:

, (3)

Отсюда радиус частицы равен

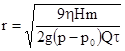, (4)

Следовательно, определяя экспериментально зависимость массы осевшего осадка от времени, можно рассчитать размер частиц.

Определение дисперсного состава суспензий, порошков, аэрозолей и других микрогетерогенных систем основано на разнообразных седиментометрических методах дисперсионного анализа.

К ним относят: отмучивание – разделение суспензии на фракции путем многократного отстаивания и сливания; измерение плотности столба суспензии, изменяющейся вследствие седиментации частиц суспензии; пофракционное (дробное) оседание; метод отбора массовых проб – один из наиболее достоверных; накопление осадка на чашке весов; электрофотоседиментометрия, основанная на изменении интенсивности пучка света, проходящего через столб суспензии, о чем судят по измерениям оптической плотности; седиментометрия в поле центробежных сил, основанная на применении центрифуг.

Для успешного проведения седиментометрического анализа должно выполняться условие независимого движения каждой частицы. Этого достигают, применяя разбавленные системы, а в некоторых случаях добавляя стабилизаторы, препятствующие слипанию частиц.

Известны и применяются в практике различные приборы – седиментометры. Например, ряд приборов позволяет проводить анализ по методу накопления осадка на чашечке весов (метод предложен Оденом). Принцип метода состоит в том, что через определенные интервалы времени взвешивают чашку, опущенную в суспензию, и по нарастанию ее массы судят о соотношении различных фракций в суспензии.

 Скачать реферат