Матричное балансовое равенство
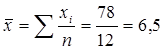 ;
; 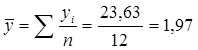
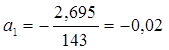 a0 = 1,97+0,02*6,5=2,1
a0 = 1,97+0,02*6,5=2,1
Yрасч= 2,1- 0,02x
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| yi | 2,12 | 2,2 | 2,11 | 2,03 | 2,21 | 1,88 | 1,91 | 2 | 1,9 | 1,99 | 1,54 | 1,74 |
| yрасч | 2,08 | 2,06 | 2,04 | 2,02 | 2 | 1,98 | 1,96 | 1,94 | 1,92 | 1,9 | 1,88 | 1,86 |
Т.о., прогнозирующее уравнение yр=2,1- 0,02x
4) Прогноз на следующие три месяца:
| xi | 13 | 14 | 15 |
| yр | 1,88 | 1,86 | 1,84 |
Строим на графике уравнение регрессии:
| x | 5 | 10 |
| y | 2 | 1,9 |
Задание 3.
Пусть необходимо выбрать один из нескольких вариантов строительства АЗС, при этом известно, что автомобили прибывают на станцию случайным образом и, если не могут быть обслужены сразу, становятся в очередь. Дисциплина очереди – «первым пришел – первым обслужен». Будем считать, что во всех вариантах рассматривается только одна бензоколонка, а вариант от варианта отличается лишь ее мощностью. Предположим также, что статистические наблюдения позволили получить величину среднего времени обслуживания одного автомобиля и средний интервал между прибытием автомобилей.
По этим статистическим данным вычислить основные показатели, характеризующие систему массового обслуживания (коэффициент простоя системы, среднее число клиентов в системе, среднюю длину очереди, среднее время пребывания клиента в системе, время пребывания клиента в очереди) и сделать вывод о целесообразности выбора варианта строительства АЗС.
| Интервал прибытия клиентов | Варианты среднего времени обслуживания | ||||
| 6 | 7,6 | 6,2 | 5,8 | 5,2 | 4 |
Решение: Имеем дело с простейшим потоком т.к., он стационарный (не зависит от его расположения на оси времени), ординарный (требования поступают по одиночке) и независимо друг от друга (отсутствие последствия).
Плотность распределения числа требований за время t имеет следующее выражение:
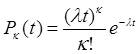
Определим l = 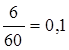 треб/мин
треб/мин
Вероятность того, что за одну минуту поступит не одно требование
P0(1)=e-0,1 = 0,9048; одно требование: P1(1) = 0,1e-0,1 = 0,0905
Интервал между двумя последовательными требованиями:
P = e-0,1t
Время обслуживания задается экспоненциальным законом с плотностью расширения g(t) = me-mt; 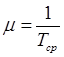
Среднее время обслуживания равно математическому ожиданию:
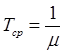
Время ожидания в очереди задается экспоненциальным законом с плотностью распределения h(t) = ne-nt; 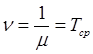
Результаты оформим таблицей:
|
Тср (мин) |
Тср (ч) (:60) |
m |
a |
P0 |
P1 |
N0 |
N3 |
K0 |
Средняя величина очереди, Mож |
Среднее число требований, M |
Вероятность того, что число требований в очереди >=1 |
|
7,6 |
0,127 |
7,874 |
0,013 |
0,987 |
0,013 |
0,987 |
0,013 |
0,987 |
0,013 |
0,026 |
0,013 |
|
6,2 |
0,103 |
9,709 |
0,010 |
0,99 |
0,010 |
0,99 |
0,010 |
0,99 |
0,010 |
0,020 |
0,010 |
|
5,8 |
0,097 |
10,309 |
0,009 |
0,991 |
0,009 |
0,991 |
0,009 |
0,991 |
0,009 |
0,018 |
0,009 |
|
5,2 |
0,087 |
11,494 |
0,008 |
0,992 |
0,008 |
0,992 |
0,008 |
0,992 |
0,008 |
0,016 |
0,009 |
|
4 |
0,067 |
15,625 |
0,006 |
0994 |
0,006 |
0,994 |
0,006 |
0,994 |
0,006 |
0,012 |
0,006 |
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
