Математическая модель системы в переменных пространства состояний

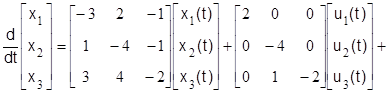
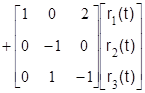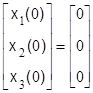, , (3.2.4)

. (3.2.5)

Решение.

Запишем для системы (3.2.4) характеристическое уравнение (3.1.1)

. (3.2.6)

Раскроем скобки и приведем подобные члены, получим следующее характеристическое уравнение:

. (3.2.7)

Устойчивость системы будем определять на основе алгебраического критерия устойчивости Гурвица, составив для этого по уравнению (3.2.7) матрицу Гурвица

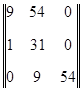. (3.2.8)

Для устойчивости линейной системы по критерию Гурвица необходимо и достаточно, чтобы при положительности коэффициента при старшей степени (в нашем случае коэффициент при λ3 равен 1) были положительными и все n диагональных определителей Гурвица, то есть Δi>0 (i=1,2,3)

, .

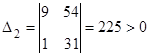В соответствии с вышеизложенным находим, что свободный член характеристического уравнения (3.2.7) равный 54 - положительный.

Следовательно, система (3.2.4) является устойчивой.

УПРАВЛЯЕМОСТЬ

ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

Управляемость системы (2.1.1), (2.1.2) по состояниям определяется теоремой (критерием) Калмана: система будет управляемой тогда и только тогда, когда ранг матрицы управляемости Lc размерности равен n, то есть

rankn, (4.1.1)

где

. (4.1.2)

Если rank<n, то система будет частично управляемой, а при rank=0 – полностью неуправляемой.

Управляемость системы (2.1.1), (2.1.2) по выходам (критерий Калмана): система будет управляемой тогда и только тогда, когда ранг матрицы управляемости размерности равен l то есть

rank=l, (4.1.3)

где

. (4.1.4)

Если rank<l, то система будет частично управляемой по выходам, а при rank=0 – полностью неуправляемой.

Показатель степени n в выражениях (4.1.2), (4.1.4) соответствует размерности вектора состояний.

4.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 4.2.1

Определить управляемость динамической системы по состояниям, заданной векторными уравнениями

,

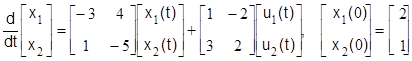(4.2.1)

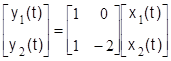. (4.2.2)

Решение.

В соответствии с выражением (4.1.2) запишем матрицу управляемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2

.

Найдем произведение матриц

.

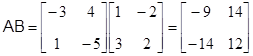Следовательно, матрица управляемости имеет вид

,

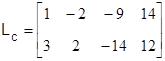и ее ранг rank2, то есть настоящая система полностью управляема по состояниям.

Задача 4.2.2

Определить управляемость по выходам динамической системы, заданной векторными уравнениями

,

.

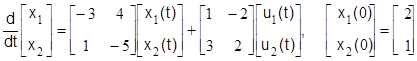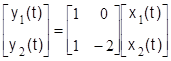Решение.

В соответствии с выражением (4.1.2) запишем матрицу управляемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2

.

Найдем произведение матриц

.

.

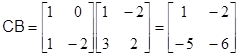Следовательно, матрица управляемости имеет вид

,

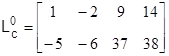и ее ранг rank=2, то есть настоящая система полностью управляема по выходам.

5. НАБЛЮДАЕМОСТЬ

5.1. ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

Наблюдаемость системы (2.1.1), (2.1.2) определяется теоремой (критерием) Калмана: система будет вполне наблюдаемой тогда и только тогда, когда ранг матрицы наблюдаемости L0 размерности равен n, то есть

rankn, (5.1.1)

где

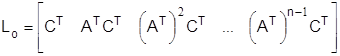. (5.1.2)

Если rank<n, то система будет не вполне наблюдаемой, а при rank=0 – полностью ненаблюдаемой.

5.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 5.2.1

Определить наблюдаемость динамической системы, заданной векторными уравнениями

.

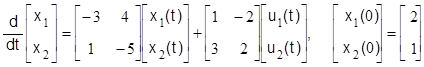
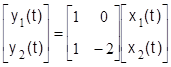Решение.

В соответствии с выражением (5.1.2) запишем матрицу наблюдаемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2

.

Найдем произведение матриц

.

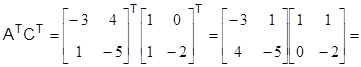
Следовательно, матрица наблюдаемости имеет вид

,

и ее ранг rank2, то есть настоящая система полностью наблюдаема.

 Скачать реферат