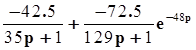Колонна для перегона коньячного спирта

2 Математическая модель установки и преобразование ее в пространство состояний

Математическая модель в виде матрицы передаточных функций приведена в таблице 2.

Таблица.2

На рисунке 2 представлена блок – схема модели колонны.

Рисунок 2 – Блок-схема модели колонны

В исходных данных, модель дана как мы видим в виде матриц передаточных фунцый. Для преобразования передаточных функций в пространство состояний использовали соотношения. Наиболее простой аппроксимацией опоздания является замена его инерционным звеном первого порядка. Для проверки правильности преобразования следует найти собственные значения системы с помощью функции Eig и убедиться, что или все собственные значения имеют отрицательные действительные части (система постоянна), или число нулевых собственных значений совпадает с числом интегральных звеньев в исходной модели. Окончательно система должна быть представлена матрицами A,B,C,D.

Рисунок 3. Развернутая структурная схема системы с учетом запаздывания

Исходя из систем получим матрицы модели в пространстве состояний

где х- состояние систем;

y- измеряемые входы;

f- возмущение;

u- управление.

Матрицы системы имеют вид:

A=[-1/35 0 0 0 0 0 0 0 0 0 0 0 0 0;

0 -1/129 0 0 0 0 0 0 0 0 0 0 0 0;

0 4/48 -2/48 0 0 0 0 0 0 0 0 0 0 0;

0 0 0 -1/38 0 0 0 0 0 0 0 0 0 0;

0 0 0 4/9 -2/9 0 0 0 0 0 0 0 0 0;

0 0 0 0 0 -1/110 0 0 0 0 0 0 0 0;

0 0 0 0 0 4/134 -2/134 0 0 0 0 0 0 0;

0 0 0 0 0 0 0 -1/13.5 0 0 0 0 0 0;

0 0 0 0 0 0 0 0 -1/98 0 0 0 0 0;

0 0 0 0 0 0 0 0 4/133 -2/133 0 0 0 0;

0 0 0 0 0 0 0 0 0 0 -1/50 0 0 0;

0 0 0 0 0 0 0 0 0 0 4/12 -2/12 0 0;

0 0 0 0 0 0 0 0 0 0 0 0 -1/186 0;

0 0 0 0 0 0 0 0 0 0 0 0 4/150 -2/150];

Матрица входа:

B=[-42.5/35 0;

-72.5/129 0;

0 0;

1720/38 0;

0 0;

730/110 0;

0 0;

0 0.994/13.5;

0 0.459/98;

0 0;

0 -6.9/50;

0 0;

0 -5.1/186;

0 0];

Матрица измерений:

C=[1 -1 1 0 0 0 0 1 -1 1 0 0 0 0;

0 0 0 -1 1 -1 1 0 0 0 -1 1 -1 1];

где матрица системы:

D=[0 0;0 0];

3 Преобразование математической модели в дискретное время и ее проверка с помощью построения разгонных характеристик

Для преобразования математической модели в дискретное время использовалась функция программного пакета Matlab c2d. При этом шаг дискретности нужно выбирать с учетом того что процессы в замкнутой системе будут проходить в 10 раз быстрее чем в объекте.

dt=0.01/max(abs(eig(A)))

t=0:dt:999;

[Ad,Bd]=c2d(A,B,dt);

dt=0.4500

Проверить найденную модель в дискретном времени следует с помощью расчета разгонных характеристик. Для этого следует использовать функцию dstep. Для вывода графиков следует использовать функции: subplot, plot, grid.

Ad =

Columns 1 through 8

0.9872 0 0 0 0 0 0 0

0 0.9965 0 0 0 0 0 0

0 0.0371 0.9814 0 0 0 0 0

0 0 0 0.9882 0 0 0 0

0 0 0 0.1892 0.9048 0 0 0

0 0 0 0 0 0.9959 0 0

0 0 0 0 0 0.0134 0.9933 0

0 0 0 0 0 0 0 0.9672

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

Columns 9 through 14

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0.9954 0 0 0 0 0

0.0135 0.9933 0 0 0 0

0 0 0.9910 0 0 0

0 0 0.1439 0.9277 0 0

0 0 0 0 0.9976 0

0 0 0 0 0.0119 0.9940

Bd =

-0.5429 0

-0.2525 0

-0.0047 0

20.2483 0

1.9628 0

2.9803 0

0.0200 0

0 0.0326

0 0.0021

0 0.0000

0 -0.0618

0 -0.0045

0 -0.0123

0 -0.0001

Построим разгонные характеристики с помощью функций dstep, subplot, plot, grid.

Рисунок 4.Кривые разгона.

В результате анализа кривых разгона можно сделать вывод, что значения полученные на выходе каналов регулирования описанных инерционными звеньями 1-го порядка совпадают со значением коэффициента К инерционного звена, а на выходе каналов регулирования представленных интегрирующим звеном, кривые разгона направлены в отрицательную сторону, если имеют знак «-» в передаточной функции звена и наоборот. Если сравнить матрицу передаточных функций и полученные разгонные характеристики, видно, что Кр совпадают, можно сделать вывод: построение модели и преобразование выполнены верно.

4 Синтез многомерного ПИ-регулятора

Для синтеза ПИ-регулятора полученные матрицы должны быть расширены в матрицы A1, B1, C1:

A1=[Ad zeros(n,l); C eye(l)];

B1=[Bd;zeros(m)];

C1=[C eye(l)];

Матрицы параметров регулятора должны быть расчитаны с помощью функции dlqr.

K=dlqr(A1,B1,Q,R)

L=dlqr(A1',C1',Q1,R1)'

Весовые матрицы Q1,R1,Q,R выбраны как единичные (для простоты матрицы генерирует функция eye).

Матрицы имеют вид:

A1 =

Columns 1 through 8

0.9872 0 0 0 0 0 0 0

0 0.9965 0 0 0 0 0 0

0 0.0371 0.9814 0 0 0 0 0

0 0 0 0.9882 0 0 0 0

0 0 0 0.1892 0.9048 0 0 0

0 0 0 0 0 0.9959 0 0

0 0 0 0 0 0.0134 0.9933 0

0 0 0 0 0 0 0 0.9672

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

1.0000 -1.0000 1.0000 0 0 0 0 1.0000

0 0 0 -1.0000 1.0000 -1.0000 1.0000 0

Columns 9 through 16

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

 Скачать реферат