Использование модели экономического цикла Самуэльсона-Хикса

дает необходимое и достаточное условие устойчивости для данного случая. Для этого требуется, чтобы выполнялось неравенство

Систему можно заменить одним неравенством

Объединяя все получ

енные результаты, условие устойчивости можно представить в виде двойного неравенства

,(13)

Уравнение модели экономических циклов Самуэльсона-Хикса имеет вид уравнения (8), при этом

Заметим, что Cy 0 и 0 в силу экономического содержания этих параметров. Согласно теореме Виета,

,(14)

Условие D = 0, разделяющее колебательные и неколебательные решения, теперь имеет вид

При характеристическое уравнение имеет вещественные корни. Из неотрицательности параметров Cy и и равенств (14) следует, что оба корня неотрицательны и обе компоненты решения (10) изменяются монотонно. При решение носит колебательный характер.

Условие устойчивости (13) теперь принимает вид

т.е. представляет собой систему неравенств

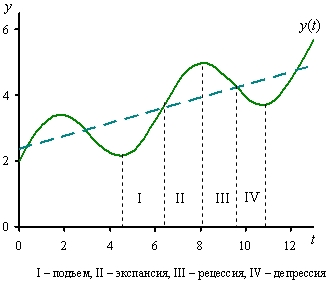
На рис. 4. устойчивому движению соответствуют области I (монотонное движение) и II (колебательное движение). Неустойчивому движению соответствуют области III (колебательное движение) и IV (монотонное). Области V соответствуют синусоидальные колебания с постоянной амплитудой.

[5]

Рис. 4. Стилизованные фазы экономического цикла

Разностные уравнения играют большую роль в экономической теории. Многие экономические законы доказывают с помощью именно этих уравнений, они используются в тех случаях, когда запаздывание оказывает существенное влияние на рассматриваемые процессы. В социально – экономических науках в целях простоты модели, связанные с запаздыванием, записывают в виде разностных уравнений, то есть в виде уравнений с дискретным временем. Наиболее широкое распространение разностные уравнения в экономической теории

Применение разностных уравнений в экономике представлено в моделях:

1. Модель рынка с запаздыванием сбыта.

2. Рыночная модель с запасами.

3. Динамическая модель Леонтьева.

4. Модель экономического цикла Самуэльсона – Хикса.

ГЛАВА 2. МОДЕЛЬ САМУЭЛЬСОНА-ХИКСА И ЕЕ ПРИМЕНЕНИЕ

2.1 Модель Самуэльсона-Хикса

Модель Самуэльсона-Хикса включает в себя только рынок благ, и поэтому уровень цен и ставка процента предполагаются неизменными; объем предложения благ совершенно эластичен.

Объем потребления домашних хозяйств в текущем периоде зависит от величины их дохода в предшествующем периоде

Ct = Ca,t + Cyyt-1,

где Ca - автономное потребление.

Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, зависящие от прироста совокупного спроса в предшествующем периоде

It = Ia,t + (yt-1 - yt-2).

На рынке благ установится динамическое равновесие, если

,(15)

где At = Сa,t + Ia,t.

Уравнение (15) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

Уравнение (9.1) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

При фиксированной величине автономных расходов (At = A = const) в экономике достигается динамическое равновесие, когда объем национального дохода стабилизируется на определенном уровне , т.е.yt = yt-1 = yt-2 = . = yt-n = , где n - число периодов с неизменной величиной автономных расходов.

Из уравнения (15) следует, что = A/(1 - Cy).

Посмотрим, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса.

Освободимся от неоднородности в уравнении (15). Значения yt и удовлетворяют равенству (15), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами:

,(16)

где yt yt - .

Так как yt = + yt, то направление изменения yt определяется направлением изменения yt.

Из теории решения дифференциальных и конечно-разностных уравнений следует, что характер изменения yt зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (Cy + )2 - 4, то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.

Если (Cy + )2 - 4 > 0, то изменение yt происходит монотонно; при (Cy + )2 - 4 < 0 оно будет колебательным. Следовательно, график функции , изображенный на рис. 5, отделяет множество сочетаний Cy, , обеспечивающих монотонное изменение yt, от множества комбинаций из значений Cy, , приводящих к колебаниям yt.

 Скачать реферат