Элементы линейной алгебры
![]() ;
;
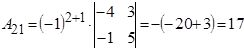 ;
;
![]() ;
;
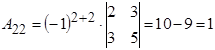 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Тогда 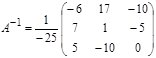
Умножим обратную матрицу на матрицу – столбец и получим искомую матрицу Х.
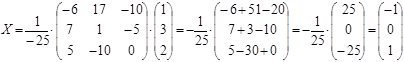
Проверка: 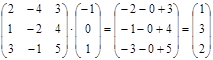 верно.
верно.
Пример 24. Найти общее и какое-нибудь частное решение системы линейных уравнений

Решение. Найдем ранг расширенной матрицы:
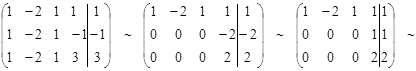
 .
.
– помножим первую строку на (– 1) и сложим поочередно со второй и с третьей строками, получим строки с тремя нулевыми элементами, результат запишем вместо второй и третьей строки соответственно.
– разделим вторую строку на (– 2) и сложим с нулевой строкой, которую мы не пишем, результат запишем вместо второй строки.
– помножим вторую строку в полученной матрице на (– 2) и сложим с третьей строкой, получим строку с нулевыми элементами, которую можно вычеркнуть.
– найдем базисный минор, не равный нулю, второго порядка, т. е. ![]() . Значит, ранги расширенной и нерасширенной матриц равны 2.
. Значит, ранги расширенной и нерасширенной матриц равны 2.
Так как ранги расширенной матрицы и матрицы системы равны между собой, но меньше числа неизвестных, то система будет иметь бесчисленное множество решений.
Возьмем два первых уравнения

Пусть z и t – главные переменные. Тогда
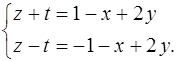
По формулам Крамера найдем значения главного и дополнительных определителей:
![]()

![]()
Тогда ![]()
![]() –
–
– общее решение системы.
Частное решение: придадим любые значения свободным переменным х и у, например, х = 1, у = 1, тогда z = 1, t = 1.
Ответ: x = y = z = t = 1.
Примеры для самостоятельного решения.
1. Вычислить определители второго порядка.
|
а) |
б) |
|
в) |
г) |
2. Решить уравнения:
|
а) |
б) |
3. Вычислить определители третьего порядка:
|
а) |
б) |
4. Вычислить определители, разложив их по элементам какой – либо строки или столбца:
|
а) |
б) |
5. Вычислить определители по правилу Саррюса или по правилу треугольников:
|
а) |
б) |
6. Вычислить определители, использовав теорему о линейной комбинации строк (столбцов):
|
а) |
б) |
7. Решить уравнение и неравенство:
|
а) Ответ: – 2,5; – 3. |
б) Ответ: |
8. Вычислить определители (используя свойства определителей) разложением по строке или столбцу:
|
а) |
б) |
9. Найти линейные комбинации матриц.
а) Если ![]() , то А – 3∙Е =. Ответ:
, то А – 3∙Е =. Ответ: ![]() .
.
б) Если ![]() и
и ![]() , то 2∙В – 5∙А =.
, то 2∙В – 5∙А =.
Ответ: ![]() .
.
в) Если  и
и  , то 4∙А – 5∙В =.
, то 4∙А – 5∙В =.
Ответ: 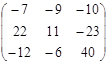 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах

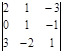 . Ответ: 4.
. Ответ: 4. 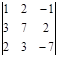 . Ответ: 0.
. Ответ: 0. 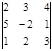 . Ответ: – 10.
. Ответ: – 10. 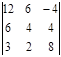 . Ответ: 72.
. Ответ: 72. 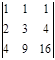 . Ответ: 2.
. Ответ: 2. 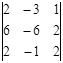 . Ответ: 10.
. Ответ: 10.  .
.
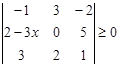 .
.
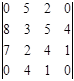 . Ответ: 60.
. Ответ: 60. 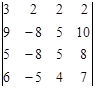 . Ответ: – 6.
. Ответ: – 6.