Элементы линейной алгебры

§ 4. Элементарные преобразования матрицы

Определение 22. Элементарными преобразованиями строк матрицы А называются преобразования следующих трех типов:

перестановка двух строк;

умножение элементов какой-либо строки на одно и то же число, отличное от нуля;

прибавление к элементам одной строки матрицы соответствующих элементов другой строки, умноженных

на число, отличное от нуля;

Аналогично определяются элементарные преобразования столбцов матрицы.

Определение 23. Матрица вида

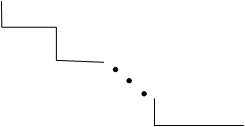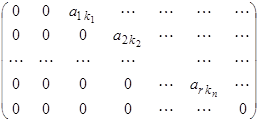называется ступенчатой.

Определение 24. Матрица В называется эквивалентной матрице А, если она получена из матрицы А путем конечного числа элементарных преобразований матрицы А. При этом пишут А ~ В.

Теорема 1. Любую матрицу можно привести к ступенчатой матрице при помощи конечного числа элементарных преобразований строк.

Обратная матрица. Матричные уравнения.

Определение 25. Обратной матрицей для квадратной матрицы А называется такая матрица А-1, которая при умножении как слева так и справа на матрицу А, дает в произведении единичную матрицу Е

А∙А– 1 = А– 1∙А = Е.

Определение 26. Квадратная матрица называется невырожденной, если ее определитель не равен нулю. В противном случае матрица называется вырожденной.

Теорема 2. Для того чтобы матрица была обратимой необходимо и достаточно, чтобы она была невырожденной.

Свойства обратной матрицы.

1. .

2. (A∙B)– 1 = B– 1∙A– 1.

3. .

I способ получения обратной матрицы основан на элементарных преобразованиях над матрицами. Составляем матрицу (А | Е) и преобразуем ее к

(Е | А– 1), т. е. (А | Е) → (Е | А– 1).

Например,

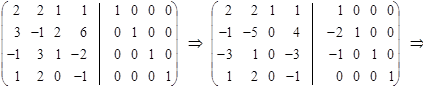
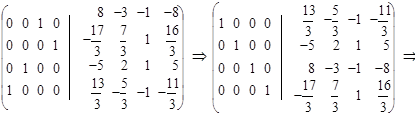
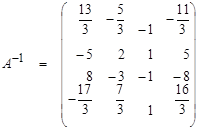
II способ нахождения обратной матрицы.

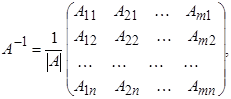(1)

где Аij – алгебраическое дополнение элементов аij данной матрицы, |А| – определитель А, причем |А| ¹ 0.

Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом

А∙Х = В (2)

Х∙А = В (3)

В этих уравнениях А, В, Х – матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.

Если в уравнениях (2) и (3) матрица А невырожденная, то их решения соответственно записываются следующим образом

Х = А– 1∙В.

Х = В∙А– 1.

§ 5. Системы линейных алгебраических уравнений

Основы теории определителей заложены в 1750 году швейцарским математиком Г. Крамером (1704–1752)

Определение 27. Системы уравнений, содержащие неизвестные только в первой степени называются линейными.

Рассмотрим систему уравнений, у которой число уравнений равно числу неизвестных

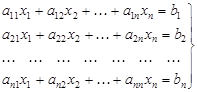, (4)

где х1, х2, …, хп – неизвестные, а11, а12, …, апп – коэффициенты (заданные числа), b1, b2, …, bn – свободные члены (заданные числа).

Если в (4) все свободные члены равны нулю, то система, имеющая вид

, (5)

называется однородной.

Система (4), в которой хотя бы один из свободных членов не равен нулю, называется неоднородной.

Решение систем линейных уравнений по формулам Крамера

Введем обозначения:

, ,

, …,

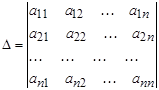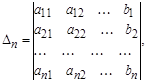
∆ – главный определитель системы (4), ∆1, ∆2, ∆3, …, ∆п – дополнительные определители, которые получаются из ∆ путем замены столбцом свободных членов элементов соответственно первого, второго, …, п – го столбцов.

Тогда формулы Крамера запишутся в виде

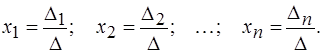(6)

Теорема 3. (о решении неоднородной системы). Возможны несколько случаев:

а) Если главный определитель системы (4) ∆ ¹ 0, то она имеет единственное решение.

б) Если ∆ = 0 и все дополнительные определители равны нулю, то система (4) имеет бесчисленное множество решений.

в) Если ∆ = 0 и хотя бы один из дополнительных определителей не равен нулю, то система (4) решений не имеет и называется несовместной.

Теорема 4. (о решении однородной системы). Возможны следующие случаи:

а) Если главный определитель однородной системы (5) не равен нулю, то эта система имеет единственное решение

х1 = х2 = … = хп = 0

называемое тривиальным.

б) Если определитель однородной системы равен нулю, то эта система имеет бесчисленное множество нетривиальных решений.

Теоремы 4, 5 играют очень важную роль, как в различных разделах математики, так и во многих практических приложениях.

Матричная запись систем линейных уравнений и ее решение.

Система уравнений (4) может быть записана в матричном виде следующим образом: А∙Х = В, где

Решение этой системы имеет вид

Х = А– 1 ∙В (det A ¹ 0).

Итак, для того, чтобы решить систему линейных неоднородных уравнений с помощью обратной матрицы надо:

записать систему линейных неоднородных уравнений в виде матричного уравнения;

Найти обратную матрицу А– 1;

Выполнить операцию умножения найденной обратной матрицы на матрицу состоящую из свободных элементов.

Ранг матрицы и его свойства.

Определение 28. Минором i – го порядка матрицы А называется определитель, составленный из элементов матрицы, расположенных на пересечении каких – либо i строк и i столбцов.

Определение 29. Рангом матрицы A называется наибольший порядок минора этой матрицы, отличного от нуля. Ранг матрицы обозначается r (A) или rang A.

Свойства ранга матрицы.

При транспонировании матрицы ее ранг не меняется.

Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

Элементарные преобразования не меняют ранга матрицы.

Ранг ступенчатой матрицы равен количеству ее ненулевых строк.

Подсчет ранга матрицы очень громоздкий. Поэтому ранг матрицы находят с помощью элементарных преобразований строк матрицы.

 Скачать реферат