Моделирование газофазных процессов, протекающих при гетерогенно-каталитическом восстановлении оксидов азота

Рис1. Движение газового потока в монолитном катализаторе.

Чтобы более детально изучить процесс на блочных катализаторах, имеет смысл воспользоваться моделированием химических процессов.

1.4. Математическое моделирование химических процессов

В прошедшее десятилетие было предпринято очень много попыток описать математически процессы, протекающие при восстановлении оксида азота.

В частности, при помощи математических моделей изучались эффекты массопереноса на блочном катализаторе. Была разработана двухмерная математическую модель для движения газового потока в слое катализатора, в которой особое внимание уделялось таким параметрам, как скорость движения потока, а, следовательно, и режим течения газового потока, диаметр монолитного канала, коэффициент диффузии и скорость химической реакции. Адекватность предложенной модели была проверена путем сравнения расчетных данных с экспериментальными. Сравнение показало, что и внутре-, и внешнедиффузионные ограничения должны приниматься во внимание, особенно при высоких температурах.

Работы этих ученых показали, что математическое моделирование процессов является очень перспективным и достаточно точным методом изучения химических процессов вообще и процессов восстановления оксидов азота в частности.

Математическая модель определяется лимитирующей стадией процесса. В случае, когда лимитирующей стадией является химическая реакция, математическая модель будет включать в себя дифференциальные уравнения первого порядка, описывающие изменение концентрации каждого вещества во времени:

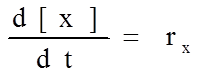
где [x] – концентрация интересующего нас вещества,

t – время,

rx – скорость изменения концентрации данного вещества во времени, имеющая, следующий вид:

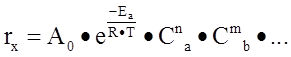
, где

- предэкспоненциальный множитель,

энергия активации процесса,

R – универсальная газовая постоянная,

С – концентрации реагентов

m, n – порядок реакции по веществам a и b соответственно. В данной работе все порядки приняты равными единице.

Если же лимитирующей стадией процесса является внутренняя или внешняя диффузия, математическая модель будет состоять из дифференциальных уравнений второго порядка. В эти уравнения входят также такие параметры, как скорость движения потока, размер пор катализатора, коэффициент диффузии. Такие зависимости позволяют определить концентрацию вещества в зависимости от длины реактора и расстояния от его оси. Вид этих уравнений представлен ниже.

Для нахождения концентрации вещества в потоке:

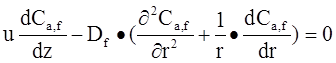
Для нахождения концентрации вещества на поверхности и внутри катализатора:

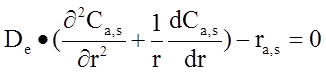
Скорость реакции разложения оксида азота описывается при помощи кинетической модели по механизму Лэнгмюра-Хиншельвуда:

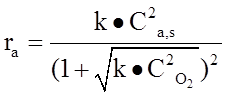
Перечень символов:

- концентрация в потоке;

- концентрация в твердой фазе (на поверхности катализатора и внутри его пор;

- коэффициент эффективной диффузии;

r – радиальная координата;

- коэффициент молекулярной диффузии;

k – константа скорости

ra – скорость реакции;

Z – аксиальная координата.

U – скорость газового потока;

1.5. Лимитирующие стадии гетерогенного каталитического процесса.

Как известно, у гетерогенной каталитической реакции может быть несколько лимитирующих стадий. Лимитирующей стадией может являться:

Внешняя диффузия реагентов или продуктов реакции. В этом случае скорость процесса будет определяться скоростью, с которой частицы реагентов из ядра газового потока будут попадать на поверхность катализатора или тем, насколько быстро образовавшиеся частицы будут уходить с поверхности катализатора в ядро газового потока.

Внутренняя диффузия реагентов или продуктов реакции. В этом случае скорость процесса определяется тем, насколько быстро молекулы реагента проникают в поры катализатора или же тем, как быстро молекулы продукта реакции освобождают пространство пор.

Адсорбция или же десорбция на поверхности катализатора. В такой ситуации скорость процесса будет определяться тем, насколько быстро происходит насыщение активных центров катализатора молекулами веществ или насколько быстро десорбируются полученные вещества с поверхности катализатора.

Непосредственно химическая реакция – в этом случае скорость процесса определяется скоростью взаимодействия веществ активных центрах катализатора.

1.6. Радикально-цепные процессы

В литературе существует ряд работ, показывающих, что большинство реальных химических реакций являются сложными и идут через посредство активных промежуточных продуктов. Реакция между двумя стабильными молекулами требует большой энергии активации. Поэтому скорость такой реакции мала. Реально наблюдаемые нами реакции идут обычно "окольными" путями, позволяющими обойти этот высокий энергетический барьер.

В случае гомогенных реакций первой стадией является обычно образование из исходных веществ тех или иных активных промежуточных продуктов. Природа этих продуктов в настоящее время еще недостаточно хорошо изучена, но, надо полагать, она может быть различной. Во многих случаях роль активных промежуточных продуктов, несомненно, играют свободные радикалы или даже свободные атомы. В других случаях это могут быть и довольно сложные и относительно стабильные молекулы, обладающие, однако, по тем или иным причинам, повышенной реакционной способностью, например, органические перекиси.

Активные промежуточные продукты, реагируя с исходными веществами, переводят их в конечные продукты реакции. Эти процессы требуют сравнительно малой энергии активации (особенно когда активными продуктами являются свободные радикалы или атомы) и идут с большей скоростью. Но первичное образование активных продуктов из стабильных исходных молекул требует большой энергии активации, и поэтому с большой скоростью проходить не может.

Для того чтобы реакция посредством активных продуктов могла протекать достаточно быстро, необходимо, чтобы активные продукты регенерировались при реакции, т.е. чтобы при взаимодействии активных продуктов с исходными веществами получались не только стабильные конечные продукты реакции, но и новые молекулы активных промежуточных продуктов. Такие реакции, в которых имеет место регенерация активных промежуточных продуктов, называются цепными(3, стр 17) Как было установлено Семеновым, Хиншельвудом и др., большинство реальных гомогенных сложных реакций являются цепными.

 Скачать реферат