Моделирование газофазных процессов, протекающих при гетерогенно-каталитическом восстановлении оксидов азота

Обозначим концентрацию активного продукта как x. Изменение этой величины со временем для цепных реакций подчиняется следующему кинетическому уравнению:

где no – скорость зарождения цепей;

f – константа скорости процесса разветвления цепей (в общем случае не совпадает с общепринятым понятием константы скорости элемента

рной реакции

g - константа скорости обрыва цепей.

Под зарождением цепей подразумевают начальный процесс образования продукта из исходных веществ, под разветвлением цепей – процесс, в котором одна молекула активного продукта, реагируя с исходными веществами, вызывает образование двух или нескольких молекул активного продукта; под обрывом цепей – процесс, при котором активный продукт безвозвратно уничтожается.

1.7. Заключение

Актуальность проблем очистки газовых выбросов от оксидов азота подтверждается значительным количеством тематических публикаций. Из литературных данных видно, что интерес исследователей к этой проблеме не угасает. Наиболее перспективными каталитическими методами удаления оксидов азота являются процессы селективного каталитического восстановления NOx с использованием в качестве восстановителей аммиака и углеводородов.

Проблема очистки газовых выбросов от NOх газов дизельных двигателей, в которых сгорание производится на “бедных” смесях, содержащих значительный избыток кислорода до сих пор не решена, т. к. в таких смесях оксиды азота обычно подвергаются окислению, а не восстановлению.

Наиболее эффективными катализаторами являются катализаторы блочного типа. Однако процессы, происходящие на таких катализаторах, по-прежнему изучены слабо. Математическое моделирование дает возможность более детально рассмотреть механизм данного процесса, оценить влияние различных стадий, а также параметров химического процесса на итоговую конверсию оксида азота, сделать предположения об условиях, в которых целесообразно будет проведение процесса.

2. ПОСТАНОВКА ЗАДАЧИ И ПОСТРОЕНИЕ МОДЕЛИ.

2.1. Экспериментальные данные.

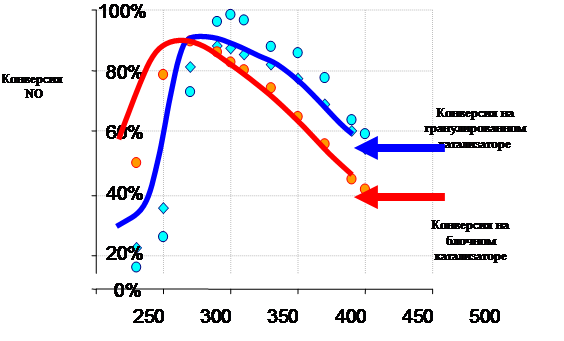На блочном катализаторе в области низких температур конверсия больше, чем на гранулированном. Гранулированный катализатор обладает большей свободной поверхностью, а, следовательно, диффузия должна быть интенсивнее, а следовательно, и конверсия выше. Значит, определяющим фактором является не диффузия, а химизм процесса.

Существуют работы …., в которых исследуется влияние свободной поверхности катализатора на конверсию оксида азота (рис 3). Существуют также экспериментальные данные, ясно указывающие на то, что конверсия оксида азота линейно уменьшается с ростом удельной поверхности катализатора.

Рис 3. Зависимость конверсии оксида азота от площади катализатора.

Учитывая наше допущение о том, что процесс восстановления оксида азота является радикальным, логично предположить, что:

· скорость продолжения цепи прямо пропорциональна свободному объему катализатора, так как с увеличением свободного объема катализатора увеличивается число образовавшихся в газовой фазе радикалов;

· скорость обрыва цепи пропорциональна доле свободной поверхности, так как с увеличением свободной поверхности катализатора все больше радикалов остается на ней, не участвуя в газофазном процессе.

2.2. Формулировка основных допущений

Схема рассматриваемой реакции:

NO + CxHy N2 + CO2

Постадийно:

CxHy + O2 + (1)

+ NO N2 + CO2 (2)

+ O2 CO2 (3)

Были сформулированы основные допущения, на основании которых создавалась математическая модель данного процесса (1,).

Лимитирующей стадией является химическая реакция.

Скорости изменения концентрации веществ описываются дифференциальными уравнениями первого порядка.

Реакция протекает с образованием свободных радикалов.

Радикалы реагируют с исходными веществами, переводя их в конечные продукты. Реакции с участием радикалов протекают по механизму, предложенному Н.Н. Семеновым.

Скорость роста цепи пропорциональна доле свободного объема катализатора

Скорость обрыва цепи пропорциональна доле свободной поверхности катализатора.

2.3. Составление математической модели

Составленная математическая модель процесса приведена ниже.

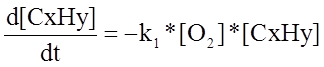
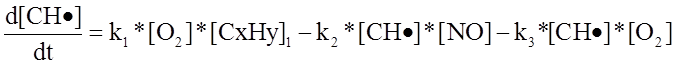где - скорость первой реакции, т. е

=

Окончательное выражение (с учетом радикальных процессов) для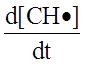

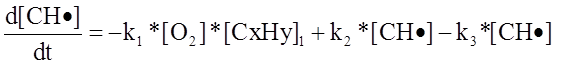
На основании составленной таким образом модели в вычислительной среде Matlab была написана программа, позволяющая отслеживать изменения интересующих нас концентраций в зависимости от двух параметров – температуры и времени. Программа решает составленные уравнения методом Рунге-Кутта четвертого порядка, результат выводится в виде графических зависимостей. Конверсия каждого вещества, участвующего в процессе, представляется как функция от выбранного параметра – времени пребывания или температуры.

 Скачать реферат