Экономико-математические методы

Остаточная дисперсия

S2 = ∑ (yi - i)2 / (n – m – 1) = 2,985 / (16 – 2 – 1) = 0,230

Ковариационная матрица:

S2 (XTX)-1 = 0,230 * =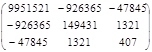

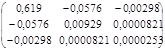
Стандартные ошибки коэффициентов равны квадратны

м корням из диагональных элементов ковариационной матрицы:

S0 = = 0,787

S1 = = 0,096

S2 = = 0,005

Проверим значимость параметров регрессии.

Табличное значение

t1 – α/2, n – 3 = 1,77

t0 = |a0| / S0 = 10,455 / 0,787 = 13,3 > 1,77

t1 = |a1| / S1 = 1,650 / 0,096 = 17,1 > 1,77

t2 = |a2| / S2 = 0,063 / 0,005 = 12,4 > 1,77

Все параметры значимы.

Коэффициент детерминации

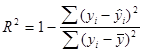= 1 – 2,985 / 125,9 = 0,976

Табличное значение критерия Фишера

Fт = 3,8

Расчетное значение

Fф = = = 267,7 > 3,8

Уравнение значимо.

Точечный прогноз:

(xp) = 10,455 – 1,650 * 3 + 0,063 * 165 = 15,83 тыс. у.е.

Интервальный прогноз

Квантиль распределения Стьюдента (по таблице)

= t0,975; 13 = 2,16

где S = = = 0,479

xp (XTX)-1(xp)T = = = 0,633

= 0,479 * = 0,381

В,Н = 15,83 ± 2,16 * 0,381 = 15,83 ± 0,68

Н = 15,15

В = 16,51

3. Экономическая интерпретация. Между возрастом автомобиля и его ценой существует тесная отрицательная связь (коэффициент корреляции –0,833): при увеличении возраста на 1 год (при фиксированной мощности двигателя) цена падает в среднем на 1,650 тыс. усл. ед.

Между мощностью двигателя и ценой автомобиля существует менее тесная положительная связь (коэффициент корреляции 0,665): при увеличении мощности на 1 л.с. (при фиксированном возрасте автомобиля) цена увеличивается в среднем на 0,063 тыс. усл. ед.

С вероятностью 0,95 можно утверждать, что цена автомобиля при возрасте 3 года и мощности двигателя 165 л.с. будет находиться в пределах от 15,15 до 16,51 тыс. усл. ед.

Задача 3

1. Для регрессионной модели

и

с помощью критерия Дарбина-Уотсона проверить наличие или отсутствие автокорреляции на уровне значимости 0,05.

2. Для регрессионной модели

проверить наличие или отсутствие мультиколлинеарности, используя:

а) парный коэффициент корреляции;

б) критерий «хи-квадрат» χ2 на уровне значимости 0,05.

Расчетная таблица:

 Скачать реферат