Производная и ее применение в экономической теории

Значит, Q=QD=200 – 4*37,5=200 – 150=50 (ед.), а

П1= – 4p2 + 300p – 5000= – 4*(37,5)2+300*37,5 – 5000=625 (ден. ед.).

2) Во втором случае прибыль была уже найдена: П2=400 (ден. ед.).

3) П=6p2 – 250p + 2500

П'=12p – 250;

12p – 250=0 Þ p=125/6=205/6 (ден. ед.).

Значит, Q=QS=6*205/6 – 100=125 – 100=25 (ед.), a

П3=6p2 – 250p + 2500=6*(205/6)2 – 250*205

/6+2500= – 1041/6 (ден. ед.).

Можно заключить, что прибыль максимальна в первом случае, следовательно, цена единицы продукции должна равняться 37,5 денежным единицам.

Задача №3: Какова максимальная выручка монополиста, если спрос вплоть до пересечения с осями описывается линейной функцией Q=b – ap, где p - цена товара, выпускаемого монополистом; a и b – коэффициенты функции спроса?

Решение: Выручка TR=Qp=p(b – ap) достигнет максимума при равенстве нулю производной по цене:

TR'=(p(b – ap))'=0.

TR'=p'*(b – ap)+ (b – ap)'*p=b – ap – ap=b – 2ap=0 Þ p= Þ

Þ Q=b – ap=b - a=.

При этом максимум выручки составит

Задача №4: Найти оптимальный объёмпроизводства фирмы, функция прибыли которой задана таким образом: П(q)=TR(q) – TC(q)=q2 – 8q + 10.

Решение: Найдём производную данной функции:

П

Приравняем производную к нулю и найдём точку экстремума:

П

Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.

При П и прибыль убывает.

При П и прибыль возрастает.

Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы.

Каким же всё-таки будет оптимальный объём выпуска для данной фирмы? Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы. Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (П(q=8)=П(q=0)=10), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования. Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.

Задача №5: Найти объём производства, при котором фирма, действующая на рынке совершенной конкуренции, будет получать максимальную прибыль, если p=15, TC(q)=q3 + 3q.

Решение: Прибыль фирмы, действующей на рынке совершенной конкуренции, максимизируется при равенстве предельной выручки и предельных издержек: MR=MC. Поскольку при совершенной конкуренции наблюдается равенство цены и предельной выручки: P=MR, то можно утверждать, что фирма максимизирует прибыль при P=MC.

Найдём предельные издержки: MC=TC'=3q2 + 3.

3q2 + 3=15;

3q2=12 Þ q=2.

Итак, мы выяснили, что при цене p=15 фирма предложит на продажу 2 единицы продукции.

Задача №6: Пусть – издержки фирмы-монополиста, QD(p)=40 – 2p – функция спроса. Найти оптимальный для данной монополии объём производства и соответствующую цену единицы продукции.

Решение: Выразим зависимость цены от количества произведённой продукции:

Тогда прибыль будет равна:

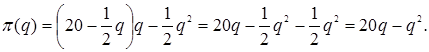
В точке q0 максимума прибыли выполняется равенство Отсюда оптимальный для монополиста объём производства равен q0=10. Соответствующая цена будет:

p0=p(q0)=

При этом предельные издержки Таким образом, цена, наиболее выгодная для данной монополии, в полтора раза выше её предельных издержек.

Задача №7: Объём продукции u цеха в течение рабочего дня представляет функцию где t – время (ч). Найти производительность труда через 2 часа после начала работы.

Решение: За период времени от t0=2 до (t0 + Dt) количество произведенной продукции изменится от u0=u(t0) до значения u0+Du = u(t0+Dt). Средняя производительность труда за этот период времени составит Du/Dt. Следовательно, производительность труда в момент t0 можно определить, как предельное значение средней производительности труда за период времени от t0 до (t0+Dt) при Dt®0, то есть

u'(t)=

Итак, производительность труда в момент времени через 2 часа после начала работы составит 43 единицы продукции в час.

Заключение

В результате проведенного исследования можно сделать следующие выводы:

1. Производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул.

2. При помощи производной можно значительно расширить круг рассматриваемых при решении задач функций.

3. Экономический смысл производной состоит в следующем: производная выступает как скорость изменения некоторого экономического процесса с течением времени или относительно другого исследуемого фактора.

4. Наиболее актуально использование производной в предельном анализе, то есть при исследовании предельных величин (предельные издержки, предельная выручка, предельная производительность труда или других факторов производства и т. д.).

5. Производная находит широкое приложение в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем (например, представляет интерес экономическая интерпретация теоремы Ферма, выпуклости функции и т. д.).

 Скачать реферат