Автокорреляционная функция. Примеры расчётов

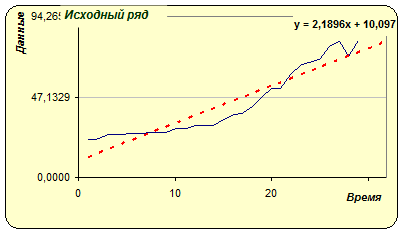
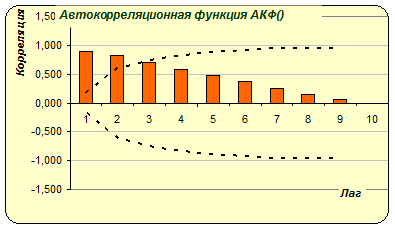
Для исходного ряда имеем:

Очевидно наличие четкого тренда, значимыми являются коэффициенты автокорреляции 1-го и 2-го порядков. Для первой разности

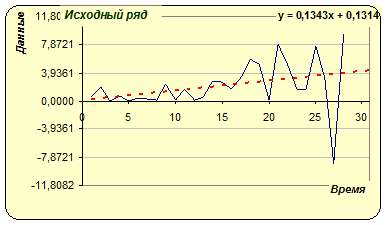
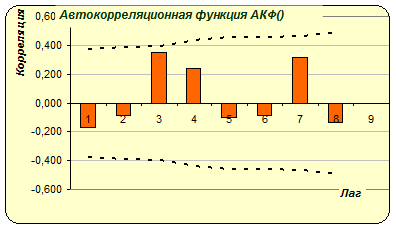
Автокорреляции уже не видим, остатки распределены как «белый шум».

Заключение

Еще одна полезная технология исследования периодичности состоит в обследовании частной автокорреляционной функции (ЧАКФ), которая представляет собой углубление взгляда обычной автокорреляционной функции.

В частной автокорреляционной функции ликвидируется зависимость между промежуточными наблюдениями. Иными словами, частная автокорреляция на данном лаге похожа на обычную автокорреляцию, исключая то, что при вычислении из нее убирается влияние автокорреляций с меньшими лагами. На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна обычной автокорреляции. Частная автокорреляция дает более «чистую» картину периодических зависимостей.

Как было отмечено ранее, периодическая составляющая для данного лага n может быть удалена взятием разности соответствующего порядка. Это обозначает, что из каждого i-го элемента ряда вычитается (i-n) – й элемент. В пользу таких преобразований имеются доводы. Во-первых, таким образом можно определить скрытые периодические составляющие ряда. Напомним, что автокорреляции на последовательных лагах зависимы. Поэтому удаление некоторых автокорреляций изменит другие автокорреляции, которые, возможно, подавляли их, и сделает некоторые другие сезонные составляющие более заметными. Во-вторых, удаление периодических составляющих делает ряд стационарным, что необходимо для применения некоторых методов анализа.

Литература

1. В.Е. Гмурман «Теория вероятностей и математическая статистика». Москва: Высшая школа, 1979 г.

2. В.Е Гмурман. «Руководство к решению задач по теории вероятностей и математической статистике». Москва: Высшая школа, 1997 г.

3. В.Н. Калинина, В.Ф. Панкин. «Математическая статистика». Москва: Высшая школа, 1994 г.

4. И.П. Мацкевич, Г.П. Свирид, Г.М. Булдык. «Сборник задач и упражнений по высшей математике (Теория вероятностей и математическая статистика)». Высшая школа, 1998 г.

5. Л.К. Тимофеева, Е.И. Суханова, Г.Г. Сафиуллин. «Сборник задач по теории вероятностей и математической статистике».

6. Тимофеева Л.К., Суханова Е.И. «Математика для экономистов». Сборник задач по теории вероятностей и математической статистике. – М.: У «Учебная литература», 1999 г.

 Скачать реферат