Экономико-математическая задача по оптимизации рационов кормления

0,1x1+0,26x2+……+0,06x10+0,6x11+0,5x12>=3,6(13)

Ограничение по содержанию витамина Е в рационе

20,9x1+50x2+……+3x11>=150(14)

Ограничение по содержанию соли в рационе

81x12>=20(15)

Дополнительные ограничения (16-25) по пределам скармливания отдельных видов кормов или групп кормов.

Условие по минимальному и максимальному удельному весу концентратов в рационе

имеет вид:

минимальная граница

(границы выбираются из таблицы 3и делятся на 100 и записываются в виде коэффициента при х13) (при x4 – коэффициент 1, в данной записи его не пишут),

(не менее 20%/100=0,2) 0,75x1+1,15x2+1,18x3+x4>=0,2x13;

максимальная граница

(не более 31 %/100=0,31) 0,75x1+1,15x2+1,18x3+x4<=0,31x13,

Исходя из этого, преобразуя неравенство (перенесем х13 за знак неравенства), получим следующую запись данных ограничений:

0,75x1+1,15x2+1,18x3+x4-0,2x13>=0 ;(16)

0,75x1+1,15x2+1,18x3+x4-0,31x13<=0,

для приведения неравенства к типу «>=», преобразуем его в следующий вид

-0,75x1-1,15x2-1,18x3-x4+0,31x13>=0(17)

Ограничение по минимальному и максимальному включению в рацион грубых кормов:

0,48x6+0,34x7-0,10x13>=0(18)

-0,48x6-0,34x7+0,25x13>=0(19)

Ограничение по минимальному и максимальному включению в рацион силоса:

0,2x9-0,12x13>=0(20)

-0,2x9+0,23x13>=0(21)

Ограничение по минимальному и максимальному включению в рацион жома:

0,12x10-0,18x13>=0(22)

-0,12x10+0,3x13>=0(23)

Ограничение по минимальному и максимальному включению в рацион сенажа:

0,32x8-0,09x13>=0(24)

-0,32x8+0,19x13>=0(25)

В данных ограничениях коэффициенты при основных неизвестных показывают содержание кормовых единиц в каждом виде корма указанной группы, а коэффициентами при вспомогательной неизвестной являются нижние и верхние границы содержания отдельных групп кормов в рационе выраженных в долях единицы,

Ограничения по максимальной суточной даче отдельных кормов (26-28) имеют следующий вид (объем ограничений выбирается из таблицы 3):

Ограничение по максимальной суточной даче патоки (не более 2 кг).

x11<=2,3(26)

Ограничение по максимальной суточной даче ВТМ (не более 1,8 кг).

x5<=1,2(27)

Ограничение по максимальной суточной даче силоса (не более 30 кг).

x9<=26(28)

Ограничения (29-30) по включению отдельных видов кормов в состав группы кормов формулируют с использованием алгебраических преобразований. Так, ограничение по включению комбикорма в размере не менее 37% (таблица 3) от веса концентрированных кормов первоначально имеет такую форму:

x4 >=0,37*(0,75x1+1,15x2+1,18x3+x4),

а после преобразований оно приобретает следующий вид:

-0,37*0,75x1-0,37*1,15x2-0,37*1,18x3+(1-0,37)x4>=0;

перемножив коэффициенты, получим:

-0,278x1-0,426x2-0,437x3+0,63x4>=0(29)

Ограничение по включению сена в группу грубых кормов в размере не менее 39 % их питательности в начале будет записано так:

0,48x6 >= 0,39*(0,48x6+0,34x7),

(0,48- 0,39*0,48)х6- 0,39*0,34x7>=0

а в окончательной форме, перемножив коэффициенты, получим:

0,293x6-0,133x7>=0 , (30)

Вспомогательное ограничение 31 , обеспечивающее нахождение суммарного количества кормовых единиц в рационе, изначально имеет вид :

0,75x1+1,15x2+,,,,,+0,76x11+0,5x12 = x13

а после преобразований оно приобретает следующий вид:

0,75x1+1,15x2+,,,,,+0,76x11+0,5x12 – x13=0 (31)

В данном ограничении коэффициенты при основных неизвестных показывают содержание кормовых единиц в каждом виде корма (табл. 1), а по вспомогательной неизвестной –1,

Целевая функция (минимум себестоимости) представлена следующим образом:

Zmin=22x1+19x2+……+3,4x10+19x11+42x12

По неизвестным, обозначающим корма собственного производства, коэффициенты показывают себестоимость 1 кг корма, а по переменным, выражающим покупные корма и добавки, - цену приобретения (табл. 4).

В матричном (развернутом) виде разработанная экономико-математическая модель представлена в таблице 5.

4 Запись экономико-математической модели в структурном виде

Целевая функция:

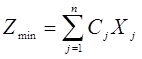, где

Cj – себестоимость или цена приобретения j-го вида корма;

Xj – искомое количество j-го вида корма в составе суточного рациона,

Ограничения (условия):

1. Питательных веществ в рационе содержится не менее необходимого количества:

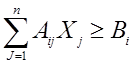, где

Aij – содержание i–го питательного вещества в единице j-го вида корма;

Bi – суточная потребность животного в i–ом питательном веществе.

2. Отдельные группы кормов включаются в рацион в зоотехнически обоснованных границах:

, где

ahj , bhj – соответственно минимально и максимально допустимый удельный вес h-ой группы кормов в общей питательности рациона, выраженной в кормовых единицах;

Ahj – содержание кормовых единиц в единице измерения j-го вида корма h- ой группы кормо.,

3. В рационе соблюдаются соотношения отдельных видов кормов и кормовых добавок

, где

Wij , W'ij–коэффициенты пропорциональности между группами кормов.

4. Вспомогательного ограничения по общему количеству кормовых единиц в единиц в рационе

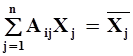, где

– суммарное количество кормовых единиц в рационе.

5. Условие неотрицательности переменных

Xj >= 0, >=0

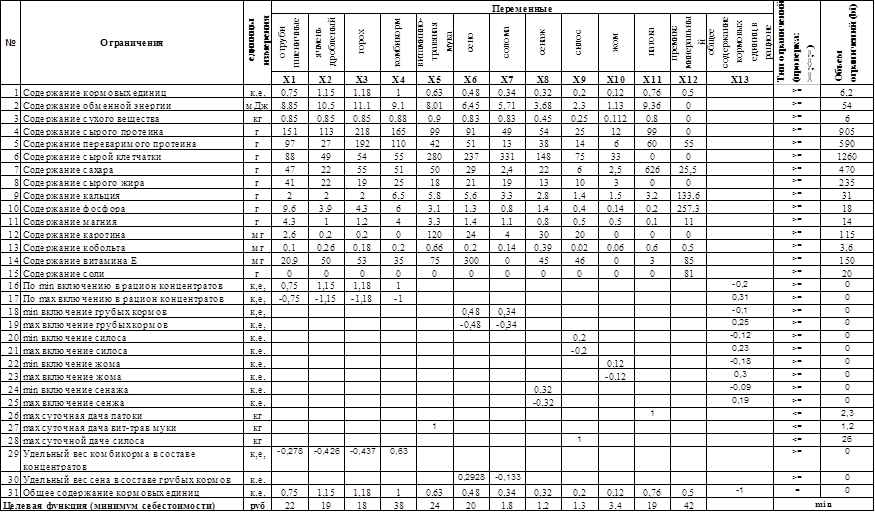
Таблица 5 Экономико-математическая модель по оптимизации рациона кормления

Дата: _ Подпись:

 Скачать реферат