Транспортные задачи

Процесс динамического программирования разворачивается от конца (т.В) к началу (т.А), а затем от т.А к т.В. В первый раз находятся условное оптимальное управление и условно минимальные затраты. Во второй раз (от т.А к т.В) определяется безусловное оптимальное управление и безусловно оптимальные затраты.

Любой путь из т.А в т.В состоит из m=4+5 отрезков. Минимальные затраты на всю операцию W

складываются из затрат на отдельных участках:

,где li затраты на i-м шаге.

Определим условное оптимальное управление.

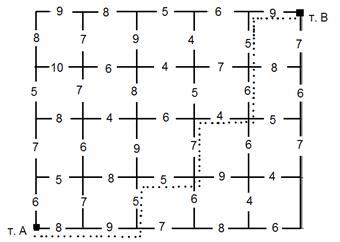
Условные минимальные затраты:

9 + 5 + 6 + 4 + 7 + 5 + 5 + 9 + 8 = 58

Теперь необходимо построить безусловное оптимальное управление т.е. двигаясь из т.А в т.В.

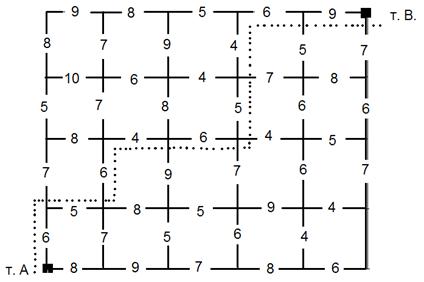
Условные минимальные затраты:

6 + 5 + 6 + 4 + 6 + 5 + 4 + 6 + 9 = 51

Задача №3

Исходные данные:

- среднее время безотказной работы Т0=2000 часов;

- среднее время восстановления Тв=1.5 часа.

Решение:

Не резервированные средства связи имеют следующие состояния:

S0 – работоспособное средство

S1 – не работоспособное средство (ремонтируется)

Размеченный граф состояний имеет вид:

Составим и решим алгебраические уравнения для финальных вероятностей:

или где:

· P0 - вероятность нахождения средства в состоянии S0 ;

· P1 - вероятность нахождения средства в состоянии S1 ;

· λ - интенсивность отказов;

· µв - интенсивность восстановления.

Нормировочное уравнение:

или

Тогда:

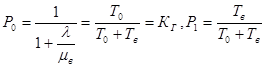
С учетом исходных данных:

Таким образом все финальные вероятности определены.

Задача №4.

Исходные данные:

· среднее время безотказной работы полукомплекта 2000 часов;

· среднее время восстановления полукомплекта Тв=2 час;

· среднее время переключения полукомплектов Тп=60 сек;

Решение:

Резервированные средства имеют следующие состояния:

· S0 – оба полукомплекта работоспособны;

· S1 – первый комплект работоспособен, а второй неработоспособен (ремонтируется);

· S2 – второй комплект работоспособен, а первый неработоспособен (ремонтируется);

· S3 – оба полукомплекта неработоспособны (ремонтируются).

Размеченный граф состояний имеет вид:

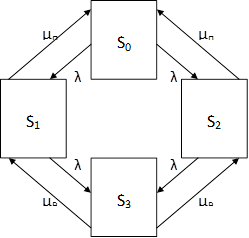
Для рассматриваемого случая линейные алгебраические уравнения Колмогорова имеют вид:

λ и µв – интенсивность отказа и восстановления.

µп – интенсивность переключения

Нормировочное уравнение имеет вид:

(5)

Из уравнений (2) и (3) видно, что . Тогда уравнение (1) запишется в виде:

или

Уравнение (4) имеет вид:

Перепишем уравнение (5) в виде:

Откуда

.

Так как 2ТпТ0 >> ТпТв , то получим:

= 2000 / 2000,03332 = 0,999998335027,

Подставив исходные данные (Тп, Т0, Тв) получим количественные данные значения Определим среднее время безотказной работы резервированной системы:

ч.

 Скачать реферат