Применение экономико-математических методов при строительстве дорог и трубопроводов

Здесь сразу уместно будет привести несколько фрагментов из воспоминаний Дейкстры. Во-первых, алгоритм этот создавался не из простого любопытства, а для решения вполне конкретной задачи, а именно, - минимизации длины проводников на аналоге "материнской платы" нового разрабатываемого командой компьютера X1, так что лавровый венок создателя первой "утилиты всех времен и народов&q

uot; класса CAD-CAE Дейкстре можно присваивать смело. А вот "во-вторых" лучше сказать словами самого Дейкстры: "На много лет и в широких кругах алгоритм поиска кратчайшего пути был основным источником моей славы, что мне всегда казалось странным - ведь он был создан даже без карандаша и бумаги, за чашкой кофе на солнечной террасе кафе в Амстердаме .".

1. ПОСТАНОВКА ЗАДАЧИ

Имеется множество географически разбросанных населенных пунктов, которых можно соединить транспортными коммуникациями. Известна стоимость строительства прямой дороги между любыми двумя пунктами (либо факт невозможности ее прокладки). Стоимость неотрицательна.

Требуется найти такой маршрут прокладки пути из заданного города в любой другой из остальных городов, чтобы он имел минимально возможную стоимость прокладки. Этот путь вполне может проходить и через несколько других пунктов.

Нашу задачу можно переформулировать следующим образом:

В ориентированной, неориентированной или смешанной (т. е. такой, где часть дорог имеет одностороннее движение) сети V найти кратчайший путь из заданной вершины i во все остальные вершины. [11]

Для решения задач такого типа – используются методы динамического программирования, теории графов, о которых пойдет речь в данной работе. Будет приведен пример решения, и программы на языке Паскаль, решающие поставленную задачу.

2. ТЕОРИЯ ГРАФОВ КАК МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ РЕШЕНИЯ ЗАДАЧ ПОДОБНОГО ТИПА

ТЕОРИЯ ГРАФОВ - это область дискретной математики, особенностью которой является геометрический подход к изучению объектов. [9] Теория графов находится сейчас в самом расцвете. Обычно её относят к топологии (потому что во многих случаях рассматриваются лишь топологические свойства графов), однако она пересекается со многими разделами теории множеств, комбинаторной математики, алгебры, геометрии, теории матриц, теории игр, математической логики и многих других математических дисциплин. Основной объект теории графов-граф и его обобщения.

Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок (задача о Кенигсбергских мостах, задача о расстановке ферзей на шахматной доске, задачи о перевозках, задача о кругосветном путешествии и другие). Одним из первых результатов в теории графов явился критерий существования обхода всех ребер графа без повторений, полученный Л. Эйлером при решении задачи о Кенигсбергских мостах. Вот пересказ отрывка из письма Эйлера от 13 марта 1736 году: ”Мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто 7 мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел лёгкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может“. Кенигсбергские мосты схематически можно изобразить так:

Рис. 1. Кенигсбергские мосты на карте, и в виде графа.

Свет вода газ

Рис.2. Задача о электро-газо-водоснабжения, схематично и в виде графа.

как “задача об электро -, газо - и водоснабжении”. В 1917 году Генри Э. Дьюдени дал ей такую формулировку. В каждый из трёх домов, изображенных на рисунке, необходимо провести газ, свет и воду.

Можно ли так проложить коммуникации, чтобы они, нигде не пересекаясь друг с другом, соединяли каждый дом с источниками электричества, газа и воды? Иначе говоря, можно построить плоский граф с вершинами в шести указанных точках? Оказывается, такой граф построить нельзя. Об этом говорится в одной очень важной теореме – так называемой теореме Куратовского. Теорема утверждает, что каждый граф, не являющийся плоским, содержит в качестве подграфа один из двух простейших пространственных графов:

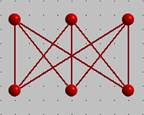
Рис. 3. Пространственные графы

В середине 19 в. появились работы, в которых при решении практических задач были получены результаты, относящиеся к теории графов. Так, например, Г. Кирхгоф при составлении полной системы уравнений для токов и напряжений в электрической схеме предложил по существу представлять такую схему графом и находить в этом графе основные деревья, с помощью которых выделяются линейно независимые системы контуров. А. Кэли, исходя из задач подсчета числа изомеров предельных углеводородов, пришел к задачам перечисления и описания деревьев, обладающих заданными свойствами, и решил некоторые из них.

В 20 в. задачи, связанные с графами, начали возникать не только в физике, химии, электротехнике биологии, экономике, социологии и т.д., но и внутри математики, в таких разделах, как топология, алгебра, теория вероятностей, теория чисел. В начале 20 в. графы стали использоваться для представления некоторых математических объектов и формальной постановки различных дискретных задач; при этом наряду с термином «граф» употреблялись и другие термины, например, карта, комплекс, диаграмма, сеть, лабиринт. После выхода в свет в 1936 году монографии Д. Кёнига термин «граф» стал более употребительным, чем другие. В этой работе были систематизированы известные к тому времени факты. В 1936 году вышла небольшая брошюра Ойстена Оре, содержащая блестящее элементарное введение в теорию графов. В 1962 году в Англии была издана книга французского математика Клода Бержа “Теория графов и её приложение”. Обе книги, безусловно, представляют интерес для любителей занимательной математики. Сотни известных головоломок, на первый взгляд не имеющих ничего общего друг с другом, легко решаются с помощью теории графов. [9]

 Скачать реферат