Применение экономико-математических методов при строительстве дорог и трубопроводов

Данное понятие грани, по - существу, совпадает с понятием грани многогранника. В качестве поверхности в этом случае выступает поверхность многогранника. Если многогранник выпуклый, его можно изобразить на плоскости, сохранив все грани. Это можно наглядно представить следующим образом: одну из граней многогранника растягиваем, а сам многогранник «расплющиваем» так, чтобы он весь поместился внутр

и этой грани. В результате получим плоский граф. Грань, которую мы растягивали «исчезнет», но ей будет соответствовать грань, состоящая из части плоскости, ограничивающей граф.

Таким образом, можно говорить о вершинах, рёбрах и гранях многогранника, а оперировать соответствующими понятиями для плоского графа.

14. Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины смежные.

15. Конечная последовательность необязательно различных рёбер E1,E2, .En называется маршрутом длины n, если существует последовательность V1, V2, . Vn необязательно различных вершин, таких, что Ei = (Vi-1,Vi ).

16. Если совпадают, то маршрут замкнутый.

17. Маршрут, в котором все рёбра попарно различны, называется цепью.

18. Замкнутый маршрут, все рёбра которого различны, называется циклом. Если все вершины цепи или цикла различны, то такая цепь или цикл называются простыми.

19. Маршрут, в котором все вершины попарно различны, называется простой цепью.

20. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.

21. Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины.

22. Любой максимальный связный подграф (то есть, не содержащийся в других связных подграфах) графа G называется компонентой связности. Несвязный граф имеет, по крайней мере, две компоненты связности.

23. Граф называется k - связным (k - реберно-связным), если удаление не менее k вершин (ребер) приводит к потере свойства связности.

24. Маршрут, содержащий все вершины или ребра графа и обладающий определенными свойствами, называется обходом графа.

25. Длина маршрута (цепи, простой цепи) равна количеству ребер а порядке их прохождения. Длина кратчайшей простой цепи, соединяющей вершины vi и vj в графе G, называется расстоянием d (vi, vj) между vi и vj.

26. Степень вершины - число ребер, которым инцидентна вершина V, обозначается D(V).

С помощью различных операций можно строить графы из более простых, переходить от графа к более простому, разбивать графы на более простые и т.д.

Среди одноместных операций наиболее употребительны: удаление и добавление ребра или вершины, стягивание ребра (отождествление пары смежных вершин), подразбиение ребра (т.е. замена ребра (u, v) на пару (u, w), (w, v), где w - новая вершина) и др.

Известны двуместные операции: соединение, сложение, различные виды умножений графов и др. Такие операции используются для анализа и синтеза графов с заданными свойствами.

27. Два графа G1=(V1;E1), G2=(V2;E2),называются изоморфными, если существует взаимно-однозначное соответствие между множествами вершин V1 и V2 и между множествами рёбер Е1 и Е2, такое, чтобы сохранялось отношение инцидентности.

Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.

29. Расстоянием между двумя вершинами связного графа называется длина кратчайшей цепи, связывающей эти вершины (в количестве рёбер).

Теорема 1.

Пусть задан граф G=(V;E),где V - множество вершин, E - множество рёбер, тогда 2[E]=Σ(V), т.е. удвоенное количество рёбер равно сумме степеней вершин.

Теорема 2. (Лемма о рукопожатиях)

В конечном графе число вершин нечетной степени чётно.

Теорема 3.

Граф связен тогда и только тогда, когда множество его вершин нельзя разбить на два непустых подмножества так, чтобы обе граничные точки каждого ребра находились в одном и том же множестве.

3.2 Свойства связных графов

1. Связный граф остается связным после удаления ребра тогда и только тогда, когда это ребро содержится в цикле.

2. Связный граф, имеющий К вершин , содержит по крайней мере К-1 ребро.

3. В связном графе любые две простые цепи максимальной длины имеет по крайней мере одну общую вершину.

4. В графе с N вершинами и К компонентами связности число рёбер не превышает 1/2(N-K)(N-K+1).

5. Пусть у графа G есть N вершин. Пусть D(G)- минимальная из степеней вершин этого графа . Тогда D(G) > 1/2 (N-1).

Связный граф без циклов называется деревом.

Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярные генеалогические деревья.

Пример (генеалогическое дерево): На рисунке показано библейское генеалогическое дерево.

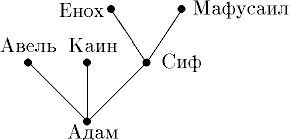
Рис. 4. Пример дерева (генеалогическое).

Эквивалентные определения дерева.

1. Связный граф называется деревом, если он не имеет циклов.

2. Содержит N-1 ребро и не имеет циклов.

3. Связный и содержит N-1 ребро.

4. Связный и удаление одного любого ребра делает его несвязным.

5. Любая пара вершин соединяется единственной цепью.

6. Не имеет циклов и добавление одного ребра между любыми двумя вершинами приводит к появлению одного и только одного цикла.

3.3 Способы задания графов

1. Геометрический:

Рис. 5. Геометрический способ задания графа

2. Матрица смежности:

Матрица смежности - квадратная матрица, размерности, равной количеству вершин. A[i,j]=1, если существует ребро (i,j) (дуга <i,j>), A[i,j]=0 - в противном случае. Для неориентированных графов матрица смежности симметрична относительно главной диагонали.

Для взвешенных графов значение элемента A[i,j] обычно используют для хранения веса соответствующего ребра. Если граф неориентированный, то матрица симметрична. Если в графе нет петель, то диагональные элементы равны 0.

 Скачать реферат