Методика факторного анализа

Задачу факторного анализа можно сформулировать следующим образом: определить минимальное число k таких факторов F1,…,Fk после учета которых исходная корреляционная матрица “исчерпается”, внедиагональные элементы ее станут близкими к нулю. Другими словами, это значит, что после учета k факторов все остаточные корреляции между исходными признаками должны стать незначимыми.

Метод главных ко

мпонент. В основе модели для выражения исходных признаков через факторы здесь лежит предположение о том, что число факторов равно числу исходных признаков (k=m), а характерные факторы вообще отсутствуют:

где величина Xj и предполагаются обладающими теми же свойствами, что и в модели (3).

Очевидно, уравнения (4) определяют здесь систему преобразования одних параметров в другие. Поскольку число факторов равно числу исходных параметров, задача искомого преобразования решается однозначно, т.е. факторные нагрузки определяются в этом методе однозначно.

Каждая из переменных Fj называется здесь i-й главной компонентой. Метод главных компонент состоит в построении факторов - главных компонент, каждый из которых представляет линейную комбинацию исходных признаков. Первая главная компонента F1 определяет такое направление в пространстве исходных признаков, по которому совокупность объектов (точек) имеет наибольший разброс (дисперсию). Вторая главная компонента F2 строится с таким расчетом, чтобы ее направление было ортогонально направлению F1 и она объясняла как можно большую часть остаточной дисперсии, и т.д. вплоть до т-й главной компоненты Fm. Так как выделение главных компонент происходит в убывающем порядке с точки зрения доли объясняемой ими дисперсии, то признаки, входящие в первую главную компоненту с большими коэффициентами оказывают максимальное влияние на дифференциацию изучаемых объектов.

Как и в центроидном методе, достаточное число компонент (факторов) определяется здесь обычно на основе некоторого заданного уровня объясненной дисперсии исходных признаков с помощью факторов (например, ).

Метод экстремальной группировки параметров. Данный метод также основан на обработке матрицы коэффициентов корреляции между исходными признаками. В основе этого метода лежит гипотеза о том, что совокупность исходных признаков может быть разбита на группы, каждая из которых отражает действие определенного фактора - причины. Поскольку признаки внутри каждой из таких групп должны быть связаны между собой более тесно, чем признаки разных групп, то задача сводится к выявлению “сильно закоррелированных” групп признаков, что позволяет выделить соответствующие факторы.

Формально задача об одновременной группировке параметров и выделении существенных факторов заключается в максимизации как по разбиению параметров на множества {A1,…,Ak} так и по выбору факторов {F1,…,Fk} одного из двух критериев.

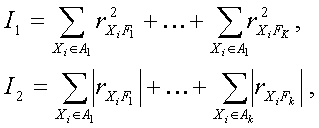(5)

где коэффициент корреляции между признаком Xi р-й группы и соответствующей ей фактором Fp , где р =1, . ,k. Таким образом, в первом случае максимируется сумма квадратов коэффициентов корреляции признаков каждой группы со 'своим' фактором, а во втором случае - сумма модулей этих коэффициентов.

Следует отметить связь метода экстремальной группировки параметров с рассмотренными выше методами факторного анализа: метод, связанный с максимизацией функционала I1, представляет естественное развитие метода главных компонент, а метод, связанный с максимизацией I2 представляет развитие центроидного метода. Так, если группы признаков зафиксированы, то в соответствии с выражением (5) в пределах каждой группы отыскивается первая главная компонента.

Характеризуя особенности этого метода, укажем, что факторы F1,…,Fk, здесь не общие для всех признаков; каждый из них соответствует 'своей' группе признаков. В отличие от методов, рассмотренных выше, факторы здесь не являются, вообще говоря, независимыми, ортогональными. Специфика экстремальной группировки параметров состоит, в частности, и в том, что в рамках этого метода каждый признак включается в один из формируемых факторов, в то время как при использовании других методов факторного анализа признаки могут относиться к нескольким факторам сразу или не принадлежать ни к одному из них.

Результаты факторного анализа будут успешными, если удается дать содержательную интерпретацию выявленных факторов, исходя из смысла показателей, характеризующих эти факторы. Данная стадия работы весьма ответственная; она требует от исследователя четкого представления о содержательном смысле показателей, которые привлечены для анализа и на основе которых выделены факторы. Поэтому при предварительном тщательном отборе показателей для факторного анализа следует руководствоваться их содержательным смыслом, а не стремлением к включению в анализ как можно большего их числа.

Применение теоремы о среднем значении в экономическом факторном анализе. Метод Лагранжа Чеботарева С.В.

Теорема Лагранжа (теорема о среднем значении) формулируется следующим образом : если функция f (x) непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка, то внутри отрезка [a;b] существует по крайней мере одна точка c, такая, что для неё выполняется равенство

f (b)-f(a)=f’(c)(b-a)

Дифференциальная теорема Лагранжа о среднем значении, записанная для функции многих переменных, позволяет перейти к формуле

Δy=Δxi

Поскольку, ci=xi+aΔ xi ( xi; xi + Δ xi) , a(0;1) то приращение функции можно представить в виде

Δy=Δxi,

где 0<<1 – параметр, который используется при анализе модели, если существует необходимость тщательного исследования всех показателей, влияющих на формирование структуры факторной системы.

Вычислив данный параметр, можно найти промежуточные значения факторов, при которых достигается точное разложение анализируемого результирующего показателя на величины факторного влияния. Если же находить не требуется, то изменение результирующего показателя вычисляется с использованием интегральной формы теоремы о среднем.

Применив интегральную форму теоремы о среднем значении для функции многих переменных, получаем формулу

Δy=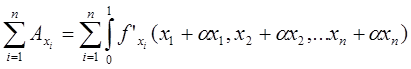Δxi

Возможность вычисления точного разложения приращения функции открывает широкие перспективы для применения формулы Лагранжа в экономическом факторном анализе, так как величины, входящие в формулу разложения приращения функции, имеют содержательную экономическую интерпретацию: приращение функции Δy есть изменение результирующего показателя, а xi и Δxi – соответственно фактор и его приращение.

 Скачать реферат