Анализ конструкции и методика расчета автомобиля ВАЗ-2105

dω = Dω kг / uГП.

При увеличении диаметра шестерни повышается прочность зуба, так как при этом больше шаг по нормали, а следовательно, и толщина зуба (примерно на 10 .15 %). Чем больше угол спирали, тем длиннее зуб и больше число зубьев, одновременно находящихся в зацеплении, по сравнению с конической передачей (примерно в 1,5 раза). Все это обусловливает снижение усилия, действую

щего на зуб, и обеспечивает высокую плавность зацепления. Кроме того, гипоидные зубчатые колеса имеют в несколько раз большее сопротивление усталости по сравнению с коническими. Перечисленные достоинства позволяют выполнить гипоидную передачу малогабаритной, а также применять ее вместо двойной на грузовых автомобилях (ЗИЛ-133Г, ЗИЛ-433100).

КПД гипоидной передачи можно найти по формуле

ηГП = (1 + μ tgβ2) / (1 + μ tgβ1)

где μ = 0,05 .0,1 — коэффициент трения между зубьями.

КПД гипоидной передачи несколько ниже КПД конической и составляет примерно 0,96 .0,97, что связано с наличием наряду с поперечным продольного скольжения зубьев со скоростью

υс.з = υ1 sin(β1 — β2) / sin β2,

где υ1 — окружная скорость шестерни. Наличие скольжения определяет весьма высокое сопротивление усталости гипоидной пары. Усталостное выкрашивание (питтинг) конических пар наблюдается в зоне чистого качения, т. е. у полюса зацепления. В гипоидных парах чистое качение отсутствует, для них характерно скольжение при высоком давлении, в связи с чем необходимо применять специальное гипоидное масло, наличие специальных присадок в котором препятствует разрушению масляной пленки.

1.4 Дифференциалы трансмиссии автомобиля

Анализ и оценка конструкции дифференциала автомобиля

На автомобиле ВАЗ-2105 применяется симметричный конический сателитный дифференциал. Симметричные конические дифференциалы наиболее распространенные (их часто называют простыми). Применяются они как на легковых, так и грузовых автомобилях, в качестве межколесных, а иногда и межосевых дифференциалов.

Для обеспечения смазки сателлитов оси в месте посадки сателлитов должны иметь лыски или спиральные канавки, удерживающие масло. Сателлиты и полуосевые шестерни выполняются прямозубыми. Число зубьев сателлитов и полуосевых шестерен может быть четным и нечетным, но для обеспечения сборки должно подчиняться условию 2zш / n = k,

где zш — число зубьев полуосевой шестерни; п — число сателлитов, k — целое число.

К преимуществам простого конического дифференциала следует отнести:

- обеспечение устойчивости при движении по скользкой дороге и торможении двигателем благодаря равенству тангенциальных реакций на ведущих колесах;

- простоту устройства, малые размеры и массу, надежность, высокий КПД.

Отрицательным качеством является ограничение проходимости.

Нагрузки в дифференциале

В коническом дифференциале определяют нагрузки на зубья сателлитов, полуосевых шестерен, крестовину и нагрузки со стороны сателлитов на корпус дифференциала.

Нагрузку на зубья сателлита и полуосевых шестерен оределяют из условия, что окружная сила распределена поровну между всеми сателлитами и каждый сателлит передает усилие двумя зубьями. Окружная сила, действующая на один сателлит,

Рс = Мкmах uкп1uгп/(r1 nс),

где r1 — радиус приложения; nс — число сателлитов (рис. 11).

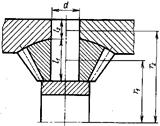
Рисунок 11. Схема сателлита

Напряжение изгиба определяется по ГОСТ 21354—87. Износ зубьев не учитывается.

Материал сателлитов и полуосевых шестерен: сталь 18ХГТ, 25ХГМ, 20ХН2М; [σи] =500 .800 MПa.

Шип крестовины (18ХГТ, 20ХНЗА и др.) под сателлитом испытывает:

- напряжение смятия

σсм = Pc/(dl1), [ σсм] =50 .60 МПа;

- напряжение среза

τср = 4Рс/(πd2), [τср] =100 .120 МПа;

- напряжение смятия в месте крепления в корпусе дифференциала под действием окружной силы Рд = Мкmах uкп1uгп/(r2 nс):

σсм = Pд/(dl2), [σсм] =50 .60 МПа.

Давление торца сателлита на корпус дифференциала определяется напряжением смятия:

σсм = Pxc / F, [σсм]=10 .20 МПа,

где Pxc = Рс tgαω sinδc (αω — угол зацепления; δc — половина угла конуса сателлита).

1.5 Силовые приводы, валы и полуоси трансмиссии автомобиля

Карданные передачи применяются в трансмиссиях автомобилей для силовой связи механизмов, валы которых не соосны или расположены под углом, причем взаимное положение их может меняться в процессе движения. Карданные передачи могут иметь один или несколько карданных шарниров, соединенных карданными валами, и промежуточные опоры. Карданные передачи применяют также для привода вспомогательных механизмов, например, лебедки. В ряде случаев связь рулевого колеса с рулевым механизмом осуществляется при помощи карданной передачи.

Методика расчёта привода трансмиссии автомобиля

Упругий полукарданный шарнир должен центрироваться, иначе балансировка карданного вала может нарушиться.

В основе всех конструкций карданных шарниров равных угловых скоростей лежит единый принцип: точки контакта, через которые передаются окружные силы, находятся в биссекторной плоскости валов.

Для пояснения этого рассмотрим простейшую модель, приведенную на рисунке 12.

Окружная скорость точки контакта О υO = ω1r1; υO = ω2r2, откуда ω1r1 = ω2r2. Подставив в это равенство значения r1 = AOsinα и r2 = BOsinβ получим ω1AOsinα = ω2BOsinβ. Угловые скорости ведущего и ведомого валов равны, если АО = ВО; α = β.

Легко показать, что в этом случае точка О лежит в биссекторной плоскости. Это видно из равенства треугольников ОО'С и OO'D.

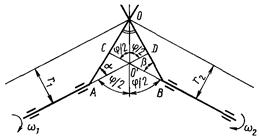
Рисунок 12. Схема карданного шарнира равных угловых скоростей

Расчет размеров деталей карданной передачи

Карданный вал. Во время работы карданный вал испытывает изгибающие, скручивающие и осевые нагрузки.

Изгибающие нагрузки возникают в результате неуравновешенности карданного вала, и в некоторой степени пары осевых сил, нагружающих шипы крестовины карданного шарнира. В эксплуатации неуравновешенность может появиться не только в результате механических повреждений карданного вала, но также при износе шлицевого соединения или подшипников карданных шарниров. Неуравновешенность приводит к вибрациям в карданной передаче и возникновению шума. Карданный вал подвергается тщательной динамической балансировке на специальных балансировочных станках. Допустимый дисбаланс зависит от максимального значения эксплуатационной угловой скорости карданного вала и находится в пределах (15 . 100) г∙см.

Даже хорошо уравновешенный вал в результате естественного прогиба, вызванного собственным весом, при некоторой угловой скорости, называемой критической, теряет устойчивость; его прогиб возрастает настолько, что возможно разрушение вала.

 Скачать реферат