Расчет планетарной коробки переключения передач трактора класса 0,2

Рефераты / Транспорт / Расчет планетарной коробки переключения передач трактора класса 0,2

nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18; nв14= nс11= nс18=0.

г). В уравнениях кинематики и связи частоты вращения всех звеньев, связанных с ведущим и ведомым валами, заменяются на nвщ и nвм . В результате уравнения кинематики [1,2.22] примут вид:

[1,2.23]

д). Для определения передаточного числа ПКП на второй передаче решаем систему уравнений [1,2.23]. Сначала из второго и третьего уравнений полученной системы уравнений [1,2.23] определяем

Поскольку и , то приравняв эти уравнения получим

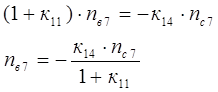
В итоге

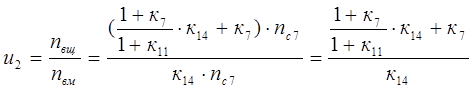
е). Для проверки выполненных аналитических выкладок в полученное уравнение из табл. 3 подставляем значения характеристик планетарных рядов . В результате получим

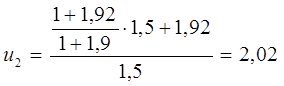
Так как полученное выражение u2 равно заданному, то вывод выражения выполнен правильно.

Определение знаков показателей степени хi b η0.

Для структурной схемы 5 ПКП согласно выражению [1,2.25],

Тогда, используя выражение [1,2.21],

Аналогично определяем

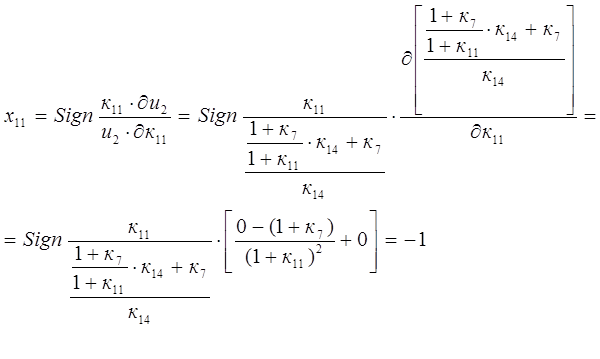
Силовое передаточное число на второй передаче определяем по выражению [1,2.20]. Тогда для структурной схемы 5 имеем

Определение КПД ПКП на второй передаче. Для структурной схемы 5 ПКП

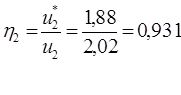
На рис. 3 приведена кинематическая схема ПКП, выполненная по структурной схеме 6 (см. рис. 2). Тормозом Т1 включается первая передача. В этом случае под нагрузкой работают планетарные ряды 7, 11 и 14. Тормозом Т2 включается вторая передача. В этом случае под нагрузкой работают планетарные ряды 7, 11 и 14. Тормозом Т3 включается третья передача. В этом случае под нагрузкой работают планетарные ряды 7, 11 и 14. Тормозом Т4 включается четвертая передача. В этом случае под нагрузкой работают планетарные ряды 7, 11, 14 и 18. Фрикционом Ф включается пятая (прямая) передача.

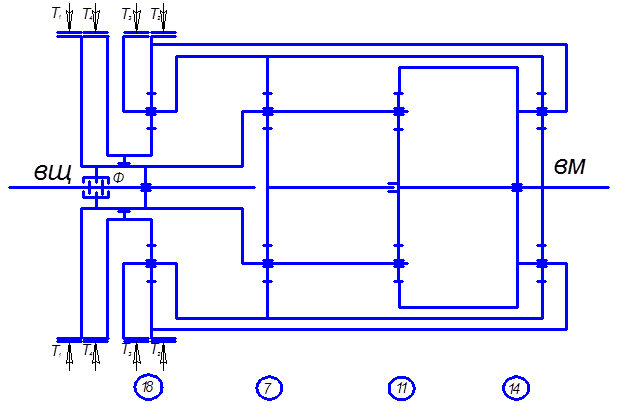
Рис. 3. Кинематическая схема ПКП

Таким образом, используя метод синтеза ПКП, выбрали наиболее рациональную ее кинематическую схему.

3. Определение чисел зубьев шестерен в планетарной коробке передач

В ТДМ, которые относятся к соосным зубчатым механизмам, нельзя произвольно назначать числа зубьев шестерен, так как необходимо, прежде всего, обеспечить совпадение осей вращения их центральных звеньев. Кроме того, при наличии нескольких сателлитов необходимо обеспечить возможность сборки механизма, а также отсутствие задевания сателлитов одного ряда друг за друга. При этом число зубьев наименьшей шестерни ТДМ должно исключать вероятность подрезания ножки зуба.

Таким образом, при подборе чисел зубьев шестерен ТДМ необходимо обеспечить соблюдение условий соосности, сборки и соседства.

Условие соосности. Выполнение этого условия обеспечивает соосность центральных зубчатых колес ТДМ. Для наиболее компактного и самого распространенного в схемах ПКП одновенцового ТДМ со смешанным зацеплением шестерен условие соосности записывается в виде:

m Zс = mZa +2 m ZB0,

где m - модуль зацепления; Zс, Za, ZB0- число зубьев соответственно солнечной шестерни, эпицикла и сателлита.

Так как модуль у всех шестерен одинаков, то

Zc=Za+2ZBo. [1,2.29]

Из условия соосности [1,2.29] вытекает важное практическое правило при подборе числа зубьев: солнечная шестерня и эпицикл должны иметь или четное или нечетное число зубьев, чтобы их разность была четной величиной. В противном случае сателлиты будут иметь дробное число зубьев.

Условие сборки. Это условие определяет возможность сборки ТДМ, т. е. возможность одновременного зацепления сателлитов с центральными зубчатыми колесами.

Рассмотрим в качестве примера одновенцовый ТДМ со смешанным зацеплением шестерен [1, рис. 2.1, а], у которого сателлит В должен одновременно находиться в зацеплении с солнечной шестерней а и эпициклом с. Это возможно только при условии, когда

[1,2.30]

где d- число сателлитов; γ- любое целое число.

Таким образом, условие сборки одновенцового ТДМ со смешанным зацеплением шестерен заключается в том, что сумма чисел зубьев солнечной шестерни и эпицикла должна быть кратна числу сателлитов.

Условие соседства. Выполнение этого условия исключает задевание сателлитов друг о друга и чрезмерные потери мощности на '"барботаж" масла (зазор между вершинами зубьев двух соседних сателлитов должен быть более 3 .5 мм). Условие соседства чаще всего проверяют графически. Установлено, что для обеспечения зазора между вершинами зубьев сателлитов более 3 .5 мм зазор между их начальными окружностями должен быть не менее 0,2 диаметра начальной окружности наименьшей шестерни планетарного ряда.

Подбор чисел зубьев необходимо начинать с наименьшей шестерни, число зубьев которой должно быть не менее 12-14. Таким образом, Zmn =12-14, что исключает вероятность подрезания ножки зуба.

В ТДМ со смешанным зацеплением шестерен и одновенцовыми сателлитами [1, рис. 2.1, а] в зависимости от характеристики к ряда меньшее число зубьев может иметь солнечная шестерня или сателлит.

Если характеристика планетарного ряда к > 3, то Zmin - на солнечной шестерне. Тогда из условия сборки [1,2.30]

[1,2.31]