Комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников

Учебные задания, способствующие формированию функциональных представлений и понятий, необходимых для осознанного усвоения понятия функции, должны характеризоваться:

1) вариативностью;

2) неоднозначностью решений;

3) нацеленностью на формирование приемов умственной деятельности (таких, как анализ и синтез, сравнение, аналогия, классификация и обобщение);

4) отображением разнообра

зных закономерностей и зависимостей;

5) включенностью их в содержательную линию курса математики начальных классов.

На основе функциональных представлений разработаны учебные задания, направленные на их формирование:

Задания на формирование представлений об изменении и зависимости: на изменение результата арифметического действия в зависимости от изменения его компонентов; на использование основного свойства дроби; на классификацию числовых выражений (равенств) на основе их результата арифметического действия; тождественные преобразования числовых выражений (равенств) на основе смысла арифметического действия; на преобразование числовых выражений; на преобразование дробных выражений; на конструирование символической модели по заданной вербальной модели и др.).

Например, «Чем похожи все пары выражений? Найди их значения:

а) 89 + 47 б) 57+29 в) 76+57

90 + 47 57+30 76+60

Сравни равенства в каждой паре и сделай вывод».

Задания на формирование представления о закономерности, как правила, по которому записаны ряды чисел: на выявление закономерности.

Например, «Найди правила, по которым составлены ряды чисел:

а) 0,5; 0,05; 0,005; 0,0005; …;

б) 0,2; 0,4; 0,6; 0,8; …;

в) 0,12; 2,14; 4,16; 6,18; ….

Запиши в каждом ряду еще три числа по тому же правилу».

Задания на формирование представления о соответствии: на соотнесение предметной, графической и символической моделей; на установление соответствия между символическими моделями.

Например, «Соедини с числом 5 те выражения, значения которых делятся на 5, если а делится на 5».

Эти учебные задания формулируются в основном на числовом материале, причем они усложняются и варьируются как по форме, так и по содержанию.

Решение задач на прямую и обратную пропорциональные зависимости посвящен решению текстовых задач на прямую и обратную пропорциональные зависимости арифметическим способом. Среди таких задач выделяются задачи, в которых числовые данные находятся в некотором отношении, что предполагает ещё один способ решения, представляющий интерес с точки зрения функциональной пропедевтики.

Кроме того, придать функциональный характер текстовым задачам можно с помощью дополнительных вопросов, направленных на изменение данных задачи, условия, вопроса, на соотнесение условия с различными выражениями и равенствами. Эти приемы помогают учащимся представить величины, рассматриваемые в задаче в движении, изменении, что позволяет формировать у учащихся функциональный стиль мышления.

На программном содержании курса математики начальных классов используются также учебные задания следующих видов:

задания на соотнесение предметной модели с числовым выражением (равенством);

задания на установление соответствия между символическими моделями;

задания на конструирование графической модели по заданной графической модели;

задания на конструирование символической модели по заданной вербальной модели;

задания на выбор символической модели, соответствующей вербальной модели;

задания на конструирование числовых равенств по заданным условиям;

задания на установление соответствия между символической и графической моделью;

задания на выбор графической модели, соответствующей символической модели;

задания на преобразование на плоскости;

задания на конструирование графической модели, соответствующей символической модели и т.д.

Приведем примеры заданий:

Задание на конструирование числовых равенств по заданным условиям:

Выбери два отношения, из которых можно составить верное равенство. Запиши это равенство:

1,5 : 2; 3 : 6; 4,5 : 8; 6 : 8; 15 : 10.

Задание на конструирование графической модели, соответствующей символической модели:

Проверь, будут ли величины х и у прямо пропорциональными при данных значениях:

Если возникнут трудности при выполнении задания, то:

представь данную таблицу в таком виде:

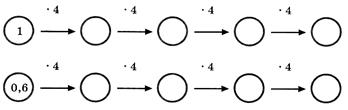
и найди отношения соответствующих значений величин х и у.

Задание на преобразование на плоскости:

Впиши пропущенные слова и числа, чтобы получились верные высказывания:

точка А (3; 4) при перемещении вправо на 2 единичных отрезка перешла в точку В (…;…);

точка L (5; -2) при перемещении на _единичных отрезков перешла в точку M (5; 2);

точка Х (1; 1) при перемещении вверх на 3 и вправо на 6 единичных отрезков перешла в точку У (…;…);

точка V (2; 3) при перемещении на _и _ на _ единичных отрезков перешла в точку W (7; -2).

4. Задание на конструирование графической модели, соответствующей символической модели:

а) Выбери единичный отрезок и построй точки в координатной плоскости:

А (0,6; 0), В (0; ), С (0,1; 0,7), D , E , К .

б) Выбери единичный отрезок и построй точки в координатной плоскости:

А(600; 0), B(0; -300), C(100; 700), E(-500; -600), K(900; -400).

Все учебные задания, обладают следующими характеристиками: вариативностью; неоднозначностью решений; нацеленностью на формирование приемов умственной деятельности (таких, как анализ и синтез, сравнение, аналогия, классификация и обобщение); отображением разнообразных закономерностей и зависимостей; включенностью их в содержательную линию курса математики начальных классов.

Таким образом, рассмотрев теоретические основы формирования представлений о функциональной зависимости у младших школьников, мы пришли к выводу, что функциональная зависимость является одной из тех математических идей, которые способны объединить в единое целое все разделы математики, включенные в школьный курс. Функциональная зависимость отражает практическую направленность курса математики, взаимосвязь величин в естественнонаучных дисциплинах, а также формирует функциональное мышление школьников. Исходя из опыта обучения, известно, что понятие функции является абстрактным и довольно сложным для восприятия учащимися. Поэтому в процессе реализации данной линии необходимо усилить наглядность изучаемых объектов и понятий в рамках отведенного времени, предоставить учащимся возможность увидеть зависимость не только в виде статичной модели, но и в динамике, дать возможность учащимся непосредственно задавать, изменять и изучать функции при помощи интерактивных моделей, расширить систему задач при помощи упражнений, содержащих анимацию и элементы управления и т.д. Такому «живому» изучению функциональной зависимости может способствовать применение комплекса упражнений, направленных на формирование представлений о функциональной зависимости.