Методика обучения решению задач на построение сечений многогранников в 10-11 классах

Введением понятия о проекционном чертеже удобно выполняется в нижеприведенной последовательности. Наиболее подходящим моментом для проведения такой работы являются уроки, непосредственно следующие за уроками, на которых доказывалась первая теорема существования и на которых учащиеся познакомились с методами построения изображений планиметрических оригиналов.

В классе устанавливается, что на

чертеже точка плоскости служит изображением не только точки оригинала, но и прямой (проектирующей). Прямая плоскости может изображать не только прямую, но и плоскость (проектирующую). Параллельные прямые плоскости изображают не только параллельные прямые оригинала, но и скрещивающиеся прямые, лежащие в параллельных проектирующих плоскостях, равно как и сами эти плоскости. Четыре точки плоскости изображений представляют, например, изображение как четырех точек одной плоскости оригинала, так и четырех точек не лежащих в одной плоскости. Внимание учащихся обращается и на тот факт, что по чертежу невозможно составить представление об относительном взаимном расположении изображенных на плоскости точки и прямой, точки и плоскости, прямой и плоскости и т.п. невозможно судить о принадлежности точек к прямым и плоскостям, прямых к плоскостям.

С неопределенностью рассматриваемых изображений можно знакомить учащихся сразу после введения понятия об изображении.

Перед введением проекционного чертежа все эти факты следует обобщить.

В качестве цели учащимся указывается на необходимость отыскания такого способа построения изображений пространственных фигур, при котором только по изображению можно было бы с безусловной необходимостью судить о взаимном расположении точек, прямых и плоскостей пространства. Прием построения изображений должен быть таким, чтобы только по изображению позволял бы определить, параллельны или непараллельны прямые оригинала, скрещиваются они или пересекаются, принадлежит точка прямой или плоскости, прямая- плоскости.

Далее учащимся сообщается, что сформулированных целей можно достигнуть, если изображения пространственных фигур, как и изображения плоских оригиналов, строить по базису с привлечением свойств изображения.

Сначала вводим понятие о базисе в оригинале и на изображении и показываем, что для построения изображения достаточно эффективно спроектировать лишь базисные точки оригинала. Далее раскрываем содержание второй теоремы существования.

К понятию проекционного чертежа можно прийти, если получить изображение одной из моделей обозначения точек в пространстве по базису и с привлечением свойств изображений.

Рассмотрим возможности осуществления этого пути на примере моделей обозначения точек с помощью основной плоскости.

Фиксировав базисные точки, строим моделей обозначения точек изображение точки. Показываем, что на таком чертеже может быть построено, и единственным образом, изображение любой наперед заданной точки оригинала.

Обосновывается и обратное утверждение, что в случае если изображение точки будет представлено вместе с основанием проектирующего отрезка на основной плоскости, то при фиксированном базисе изображение определяет единственную точку.

Как результат проведенных построений дается определение заданной точки: «Точка называется заданной на изображении, если при фиксированных базисах она является изображением единственной точки оригинала».

На построенном нами изображении заданными окажутся не только те точки, изображение которых предварительно было построено по оригиналу, но и те точки, для которых одна из точек плоскости принята за изображение собственно точки оригинала, а другая – за изображение ее основания.

Полученный таким образом проекционный чертеж представляет метрически определенное изображение.

Прямые плоскости оказываются заданными на изображении в том же смысле, что и точка.

Введение проекционного чертежа и решение задач на построение на нем не должно рассматриваться как два отдельных этапа обучения.

Одной из трудностей обучения решению задач на построение на проекционном чертеже является отсутствие в существующей учебной литературе достаточного числа четко выделенных простейших задач, овладение которыми обеспечивало бы понимание учащимися приемов решения более сложных задач. Кроме того, в методике не определилось еще число достаточно принципов, которыми можно было бы руководствоваться при отыскании решения задач.

Достижением осознанного понимания изучаемого материала при любой структуре обучения станет возможным, если решение задач не будет ограничиваться только механическим выполнением построений. От учащихся необходимо требовать устных пояснений по ходу выполняемых построений, аргументированного обоснования их. Следует также добиваться, чтобы и построения, проводимые в контрольных работах, сопровождались письменными объяснениями.

Задачи, решаемые при введении проекционного чертежа

Первой группой таких задач является упражнения, раскрывающие, что неопределенность восстановления оригинала по чертежу устранена на проекционном чертеже. Учитель показывает, что на проекционном чертеже «точка» изображает только точку оригинала, «прямая» - прямую, «плоскость» - плоскость.

На проекционном чертеже становится возможным определять только по изображению взаимное расположение точек, прямых и плоскостей. В порядке упражнения с учащимися рассматриваются способы изображения различных случаев взаимного расположения точки и основной плоскости.

В ходе упражнений учащимся сообщаются и новые необходимые определения.

В этот период следует дать определения «следа» прямой и заданной плоскости. Определения записываются в тетради.

Определение. Следом заданной прямой (плоскости) на основной плоскости называется точка (прямая) пересечения прямой (плоскости) с основной плоскостью.

В итоге обучения решению этих задач учащихся следует познакомить с двумя принципами, на основе которых выполняется построение точек пересечения прямой с плоскостью и построение прямой, по которой пересекаются плоскости.

1) для построения линий пересечения двух плоскостей достаточно знать две точки прямой, по которой пересекаются плоскости, или одну точку и направление прямой. Точки прямой, по которой пересекаются плоскости, определяются как точки пересечения произвольной прямой одной из заданных плоскостей с другой плоскостью.

2) для построения точки пересечения прямой с плоскостью достаточно построить линию пересечения произвольной вспомогательной плоскости, проведенной через данную прямую, с данной плоскостью. Точка пересечения данной прямой с данной плоскостью определяется как точки пересечения данной прямой с линией пересечения вспомогательной и данной плоскостей.

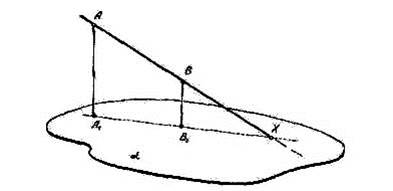Задача: Построить точку пересечения данной прямой АВ (А1В1) с основной плоскостью