Методика обучения решению задач на построение сечений многогранников в 10-11 классах

Секущая плоскость определяется парой пересекающихся прямых АВ и ММ (рис. 12) и при построении сечения правильной шестиугольной пирамиды плоскостью, проходящей через данную точку М1 основания пирамиды, параллельно одной из больших диагоналей основания и

	ight=147 src="images/referats/28696/image020.jpg">

Рис. 12

Выделение секущей плоскости — один из важных этапов решения задач на построение сечений.

При решении задач на построение сечений в доходчивой форме удается познакомить учащихся с понятиями полного и метрически определенного изображений, с решением позиционных и метрических задач.

Изображение многогранников вводится как метрически определенное в соответствии с вышеизложенной методикой обучения построению изображений. К понятию полного изображения можно подвести учащихся, если добиться от них понимания, что изображение, построенное по наперед заданному оригиналу, есть в то же время изображение более широкого класса фигур. Учащиеся должны понимать, что изображение, например, правильного тетраэдра является вместе с тем и изображением всех треугольных пирамид. Изображение правильной четырехугольной призмы, высота которой в два раза больше стороны основания, является в то же время и изображением четырехугольных призм, в основании которых, лежит не только квадрат и высота которых не только в два раза больше стороны основания, изображением не только прямых призм, но и наклонных.

Навык в построении сечений целесообразнее вырабатывать на полных изображениях, не связывая себя без необходимости с оригиналами наперед заданной формы. Это тем более полезно, что на полных изображениях раскрываются и некоторые общие свойства многогранников.

Полезно, например, не только построить сечение правильной треугольной призмы (рис 13) секущей плоскостью А102С1, где 02— середина оси призмы, но и доказать, что плоскость пересечет верхнее и нижнее основания любой из правильных треугольных призм

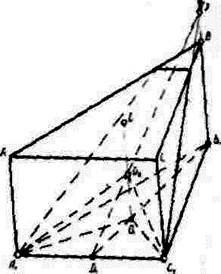
Рис. 13

Для построения сечения достаточно найти точку (X) пересечения ребра ВВ1, с прямой О102, по которой пересекаются вспомогательная плоскость BВ1DO1 с секущей плоскостью. Отрезок XB1=30102, так как D1B1 =3D1O1, и, следовательно, D1O2 пересечет верхнее основание.

Широкие возможности для проведения такой работы представляет построение изображений к задачам с буквенными данными.

Приведем в качестве примера решение задачи на построение сечения призмы плоскостью.

Задача. Построить сечение пятиугольной призмы плоскостью, заданной тремя точками, лежащими на боковых ребрах призмы.

Пусть дана призма ABCDEA'B'C'D'E' и три точки М, N, Р, лежащие соответственно на ребрах АА', ЕЕ', DD', (рис).

Выберем плоскость А'В'С нижнего основания за основную плоскость а, а направление боковых ребер — за направление проектирования на основную плоскость. При таком выборе основной плоскости и направления проектирования изображение призмы является полным, т. е. все элементы призмы (грани, ребра и вершины) заданы на чертеже, что легко проверить. Так как изображение является полным, то требуемое в задаче построение осуществимо на чертеже.

Задача построения сечения сводится в нашем случае к отысканию точек пересечения плоскости MNP с боковыми ребрами (проектирующими прямыми) ВВ' и СС.

Приведем символическую запись хода решения задачи

(L С MN, α) и (К С NP, α) Þ (MNP ∩ α = KL);

R С C'D', KL;

(R С C D') и (CD' С С CD) => (R С С CD);

(R С KL) и (KL MNP)=>(R С MNP);

(P С MNP, С CD) и (R С MNP, C'CD)=>(MNP ∩C'CD=

= PR);

(X С C'C, PR) Þ (X = MNP ∩ C C);

S С B'C, KL;

(S С B'C) и (B'C B'BC) => (S С B'BC);

(S С KL) и (KL С MNP)=>(S С MNP);

10) (XMNP,B'BC)и(SСMNP,B'BC)=>(XS=MNP∩B'BC);

11) (Y С XS, B'B)=>(Y С MNP, B'B).

Итак, MNPXY — искомое сечение.

Задача 2. Найти линию пересечения четырёхугольной пирамиды SA1B1C1D1 с плоскостью Q, проходящей через точки L(L1), М (М1) и N(N1) (рис.15).

Рис 15.

Так как точки L, М и N заданы на чертеже своими изображениями и изображениями своих внутренних центральных проекций, то в данном случае целесообразно воспользоваться центральным проектированием на плоскость П из точки S, как из центра, и определять точки пересечения рёбер пирамиды с плоскостью Q. Рёбра пирамиды здесь тоже можно рассматривать как проектирующие прямые.

Соединим точки L1 с N1, L с N и А1 с М1, затем через

точкуРх=L1N1∩A1M1 проведём проектирующую прямую SP1 и найдём точку Р=LN∩SP1. Далее,прямую MP продолжим до пересечения в точке А с ребром SA. Точка А есть точка пересечения ребра SA1 с плоскостью Q.

Черт. 51.

Чтобы найти точку D пересечения ребра SD1 с плоскостью Q, через точку R1 =A1M1∩L1D1 проведём проектирующую прямую SR1, пересекающую прямую AM в точке R, и прямую LR продолжим до пересечения с ребром SD1.

Аналогично можно найти точки В и С. Но мы здесь для определения точки С использовали точку Т=АМ ∩ ST1 и для построения точки В нашли линию SK1 пересечения граней SA1D1 и SB1C1, а точку К= SK1 ∩ AD соединили с точкой С. Отметим, что эти приёмы могут быть использованы при проверке построений. Линия ABCD есть искомая линия пересечения данной пирамиды с плоскостью.