Различные способы создания моделей правильных многогранников

Введение

На свете есть еще геометрия, которая ждет, чтобы ее познали и оценили… Так давайте же вновь перелистаем Евклида, познакомимся с некоторыми новыми результатами. Быть может, мы вновь сумеем испытать тот же восторг и трепет, как и при первых встречах с геометрией.

Самуэль Грейтцер

Есть в школьной геометрии особые темы, которые ждешь с нетерпением, предв

кушая встречу с невероятно красивым материалом. К таким темам можно отнести "Правильные многогранники". Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные научные гипотезы.

Сведения о правильных многогранниках присутствуют в программах многих учебных предметов. Возникает необходимость создания моделей правильных многогранников, а для этого требуется изучение их свойств и свойств разверток, а также методов оригами. В этом, на мой взгляд, и заключается актуальность данной темы. Таким образом, передо мной была поставлена проблема: изучить различные способы создания моделей правильных многогранников.

Цель моего исследования: расширить систему собственных знаний о правильных многогранниках. В рамках достижения поставленной цели мной будут решаться следующие задачи:

1) знакомство с информацией по теме в различных источниках;

2) изучение различных теорем о свойствах правильных многогранников и их развертках;

3) поиск различных методов оригами для создания моделей правильных многогранников;

4) изготовление моделей правильных многогранников с помощью разверток и методами оригами.

Краткое описание работы

В данной научно-исследовательской работе рассматриваются: классификация многогранников, более подробно - виды правильных многогранников, их свойства, теоремы о развертках выпуклых многогранников, Коши и Александрова. Изучены различные способы для создания моделей правильных многогранников: с помощью разверток и методами оригами. Результаты данных исследований были применены на практике, были созданы различные модели правильных многогранников. Полученные модели могут быть использованы на различных уроках и факультативных занятиях как наглядно-иллюстративный материал, а так же, как материал для дальнейших исследований всех заинтересовавшихся.

Краткий обзор используемой литературы и источников

При изучении вопросов: определение многогранника, классификация многогранников, виды правильных многогранников, их свойства я опиралась на книги: «Геометрическая рапсодия» Левитина К.Е. и Энциклопедический словарь юного математика.

Изучить теоремы о свойствах разверток выпуклых многогранников мне помогли лекции для школьников 9-11 класса Малого мехмата, изложенные в книге: «Жемчужины теории многогранников» Н.П.Долбилина.

Сложнее, оказалось, найти пособия, в которых бы излагались методы оригами для построения моделей правильных многогранников. В материалах VII Сибирской конференции «Оригами в учебном процессе» я обнаружила универсальный модуль Шеремет Г.Г. для создания моделей тетраэдра, октаэдра и икосаэдра. На сайте http://origamisan.com я нашла схемы для создания моделей из квадратного куска бумаги, которые оказались очень просты в применении. Но больше всего различных методов и идей я почерпнула из книги «Polyhendron Origami For Beginners» Miyuki Kawamura. Книгу мне пришлось изучать на английском языке, но материал в ней изложен очень доступно и интересно.

Теоретическая часть

1. Определение и классификация многогранников

Теория многогранников, в частности выпуклых многогранников, - одна из самых увлекательных глав геометрии.

Л.А. Люстерник

Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники - простейшие фигуры на плоскости. С чисто геометрической точки зрения многогранник – это часть пространства, ограниченная плоскими многоугольниками – гранями. Стороны и вершины граней называют рёбрами и вершинами самого многогранника. Грани образуют так называемую многогранную поверхность. На многогранную поверхность обычно накладывают такие ограничения:

1) каждое ребро должно являться общей стороной двух и только двух граней, называемых смежными;

2) каждые две грани можно соединить цепочкой последовательно смежных граней;

3) для каждой вершины углы прилежащих к этой вершине граней должны ограничивать некоторый многогранный угол.

Геометрические тела

Многогранники

Не многогранники

Фигура на рисунке 1 является многогранником. Совокупность из 18 квадратов на рисунке 2 многогранником не является, потому что не выполняются ограничения, накладываемые на многогранные поверхности.

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой из его граней.

Многогранник называется правильными, если:

- он выпуклый;

- все его грани являются равными правильными многоугольниками;

- в каждой его вершине сходится одинаковое число граней;

- все его двухгранные углы равны.

2. Виды правильных многогранников

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»

Л. Кэррол

2.1 Первые упоминания о правильных многогранниках

Школе Пифагора приписывают открытие существования 5 типов правильных выпуклых многогранников. Позже в своем трактате «Тимей» другой древнегреческий ученый Платон изложил учение пифагорейцев о правильных многогранниках. С тех пор правильные многогранники стали называться Платоновыми телами. Правильным многогранником посвящена последняя, XIII книга знаменитого труда Евклида «Начала». Существует версия, что Евклид написал первые 12 книг для того, чтобы читатель понял написанную в XIII книге теорию правильных многогранников, которую историки математики называют «венцом «Начал». Здесь установлено существование всех пяти типов правильных многогранников и доказано, что других правильных многогранников не существует.

2.2 Почему их только 5

А все-таки, почему же правильных многогранников только пять? Ведь правильных многоугольников на плоскости – бесконечное число.

а) Пусть грани правильного многогранника – правильные треугольники, каждый плоский угол при этом равен 60о. Если при вершине многогранного угла n плоских углов, то 60о n < 360o , n < 6,

n = 3, 4, 5, т.е. существует 3 вида правильных многогранников с треугольными гранями. Это тетраэдр, октаэдр, икосаэдр.

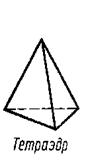
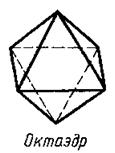
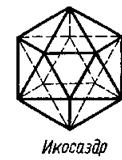
б) Пусть грани правильного многогранника – квадраты, каждый плоский угол составляет 90о. Для n – гранных углов 90о n<360о, n < 4,

 Скачать реферат