Алгебра и начало анализа

Ответ № 10
- Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией.
- Из определения арифметической прогрессии следует, что разность меж
ду любым ее членом и ему предшествующим равна одному и тому же числу, т. е. а2 - а1 = а3 - а2 = . = ak - ak-1 = . . Это число называется разностью арифметической прогрессии и обычно обозначается буквой d.
- Для того чтобы задать арифметическую прогрессию (аn), достаточно знать ее первый член а1 и разность d.
- Если разность арифметической прогрессии - положительное число, то такая прогрессия является возрастающей; если отрицательное число, то убывающей. Если разность арифметической прогрессии равна нулю, то все ее члены равны между собой и прогрессия является постоянной последовательностью.
- Характеристическое свойство арифметической прогрессии. Последовательность (аn) является арифметической прогрессией тогда и только тогда, когда любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, т. е.
 (1)
(1) - Формула n-го члена арифметической прогрессии имеет вид: an = a1 + d(n-1). (2)
- Формула суммы n первых членов арифметической прогрессии имеет вид:
 (3)
(3) - Если в формулу (3) подставить вместо аn его выражение по формуле (2), то получим соотношение

- Из определения разности арифметической прогрессии следует, что a1 + an = a2 + an-1 = ., т. е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.
Ответ № 11
- Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией.
- Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. b2:b1 = b3:b2 = . = bn:bn-1 = bn+1:bn = . . Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.
- Для того, чтобы задать геометрическую прогрессию (bn), достаточно знать ее первый член b1 и знаменатель q.
- Если q > 0 (
 ), то прогрессия является монотонной последовательностью. Пусть, например, b1= -2, q = 3, тогда геометрическая прогрессия -2, -6, -18, . есть монотонно убывающая последовательность. Если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.
), то прогрессия является монотонной последовательностью. Пусть, например, b1= -2, q = 3, тогда геометрическая прогрессия -2, -6, -18, . есть монотонно убывающая последовательность. Если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью. - Характеристическое свойство геометрической прогрессии. Последовательность (bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.
 (1)
(1) - Формула n-го члена геометрической прогрессии имеет вид:
 (2)
(2) - Формула суммы п первых членов геометрической прогрессии имеет вид:
 ,
,  (3)
(3) - Если в формулу (3) подставить вместо bn его выражение по формуле (2), то получится соот-ношение.
 ,
,  (4)
(4) - Из определения знаменателя геометрической прогрессии следует, что b1bn = b2bn-1 = …, т.е. произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная.
Сумма бесконечной геометрической прогрессии при ![]()
- Пусть (xn) - геометрическая прогрессия со знаменателем q, где
 и
и  . Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию
. Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию  , называется предел суммы n первых ее членов при
, называется предел суммы n первых ее членов при  .
. - Обозначим сумму бесконечной геометрической прогрессии через S. Тогда верна формула
 .
.
№ 12
Решение тригонометрических уравнений вида sin(x) = a
- формула для корней уравнения sin(x) = a, где
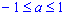 , имеет вид:
, имеет вид:  Частные случаи:
Частные случаи: - sin(x) = 0, x =
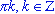
- sin(x) = 1, x =

- sin(x) = -1, x =

- формула для корней уравнения sin2(x) = a, где
 , имеет вид: x=
, имеет вид: x= 
Решение тригонометрических неравенств вида sin(x) > a, sin(x) < a
- Неравенства, содержащие переменную только под знаком тригонометрической функции, называются тригонометрическими.
- При решении тригонометрических неравенств используют свойство монотонности триго-нометрических функций, а также промежутки их знакопостоянства.
- Для решения простейших тригонометрических неравенств вида sin(x) > a (sin(x) < а) используют единичную окружность или график функции y = sin(x). sin(x) = 0 если х =
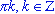 ; sin(x) = -1, если x =
; sin(x) = -1, если x =  >; sin(x) > 0, если
>; sin(x) > 0, если  ; sin(x) < 0, если
; sin(x) < 0, если  .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Loading
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
