Алгебра и начало анализа

1. Для облегчения запоминания приведенных формул нужно использовать следующие правила: a) при переходе от функций углов 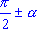, 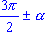к функциям угла назван

   ие функции изменяют: синус на косинус, тангенс на котангенс и наоборот; при переходе от функций углов , к функциям угла название функции сохраняют; б) считая острым углом (т. е. ), перед функцией угла ставят такой знак, какой имеет приводимая функ-ция углов , , .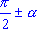

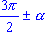Все вышеприведенные формулы можно получить, пользуясь следующим правилом: Любая тригонометрическая функция угла 90°n + по абсолютной величине равна той же функции угла , если число n - четное, и дополнительной функции, если число n - нечетное. При этом, если функция угла 90°n + . положительна, когда - острый угол, то знаки обеих функций одинаковы, если отрицательна, то различны.

№ 16

1. Формулы косинуса суммы и разности двух аргументов: Рис.1 Рис.2 Повернем радиус ОА, равный R, около точки О на угол и на угол (рис.1). Получим радиусы ОВ и ОС. Найдем скалярное произведение векторов и . Пусть координаты точки В равны х1 и y1, координаты точки С равны х2 и y2. Эти же координаты имеют соответственно и векторы и . По определению скалярного произведения векторов: = х1х2 + y1y2. (1) Выразим скалярное произведение через тригонометрические функции углов и . Из определения косинуса и синуса следует, что х1 = R cos , y1 = R sin , х2 = R cos , y2 = R sin . Подставив значения х1, х2, y1, y2 в правую часть равенства (1), получим: = R2cos cos + R2sin sin = R2(cos cos + sin sin). С другой стороны, по теореме о скалярном произведении векторовимеем: = cos BOC = R2cos BOC. Угол ВОС между векторами и может быть равен - (рис.1), - ( - ) (рис.2) либо может отличаться от этих значений на целое число оборотов. В любом из этих случаев cos BOC = cos ( - ). Поэтому = R2 cos ( - ). Т.к. равно также R2(cos cos + sin sin), то cos( - ) = cos cos + sin sin. cos( + ) = cos( - (-)) = cos cos(-) + sin sin(-) = cos cos - sin sin. Значит, cos( + ) = cos cos - sin sin.
2. Формулы синуса суммы и разности двух аргументов: sin( + ) = cos( /2 - ( + )) = cos(( /2 - ) - ) = cos( /2 - ) cos + sin( /2 - ) sin = sin cos + cos sin. Значит, sin( + ) = sin cos + cos sin. sin( - ) = sin( + (-)) = sin cos(-) + cos sin(-) = sin cos - cos sin. Значит, sin( - ) = sin cos - cos sin.

 Скачать реферат