Анализ и моделирование методов когерентной оптики в медицине и биологии

Изменения в размере объекта и его ориентации (относительно оптической оси) важны в разной степени для объектов разной формы, например вращение не оказывает существенного влияния при распознавании клеток, обладающих осевой симметрией. В любом случае вращение и изменение размера может быть выполнено либо физически, либо оптически (например, вращением «призмы Довэ), чтобы привести объект в соответ

ствие с тест-объектом. Можно преобразовать преобразование Фурье в преобразование Меллина (инвариантное к масштабу объекта), а также и получить преобразование, инвариантное к вращению [1.73], путем соответствующего воздействия на входное изображение перед обработкой.

6.2 Применения

Имеются два тина областей применения когерентных оптических методов распознавания образов: во-первых, когда сцена, объект или образ очень сложны, чтобы можно было использовать удобные цифровые методы, и, во-вторых, когда высокая скорость измерения объекта исключает применение цифровых методов. В обоих этих случаях оптическое распознавание оказывается необходимым решением. Оптическое распознавание образов также является очевидным подходом к решению проблемы, когда измерения, которые должны быть выполнены, по своей природе оказываются оптическими.

Показательным применением когерентной оптики является автоматический счет ретикулоцитов с помощью согласованных фильтров, синтезированных на ЭВМ. Квалифицированный техник может сосчитать до 500 штук в минуту. С помощью когерентной оптики мы можем обработать почти мгновенно 1 млн. (это соответствует числу ретикулоцитов на площади реального предметного стекла диаметром 1,5 см) [1.74]. В данном случае используется параллельная обработка всех освещаемых клеток. Следовательно, метод работает благодаря наличию большого числа клеток, определенные усредненные свойства которых оказываются априори известными. Например, в большом поле с объектами спичкообразной формы часть этих объектов, ориентированная вертикально с точностью ±5°, предсказывается с высокой точностью. И наоборот, если мы измеряем число, таким образом, ориентированных объектов спичкообразной формы, мы можем подсчитать их полное число. Используемые в рассматриваемом случае пространственные фильтры искали определенные обобщенные образы ретикулоцитов, по всей вероятности, не заключающие в себе точно любую клетку, а Достаточно хорошо отображающие много клеток, чтобы обеспечить основу для счета. Реальный фильтр, несколько идеализированный, синтезировался на ЭВМ.

Другое применение, которое было продемонстрировано, связано с отображением рентгеновских изображений грудной клетки для постановки диагноза пневмокониоза (затемнения легкого) [1.75]. В этом случае критерием является увеличение высокочастотных компонент в пространственном спектре тенеграммы объекта с пневмокониозом. Аналогичные измерения были выполнены над рядом других изображений, интересующих медиков.

Вероятно, самым интересным применением для обработки данных была идентификация клеток (например, видов лейкоцитов) в жидкой системе [1.76]. В данном случае не формируется никакого изображения. Для освещения отдельных клеток используется свет разных длин волн, освещающий клетки при прохождении ими точки с фиксированным освещением. Часть света, дифрагированная каждой клеткой под разными углами, является мерой размеров и формы клеток. Поскольку обрабатывается большое число клеток, то статистический анализ может быть вполне точным. Конечно, перемещение объекта (всегда присутствующее по определению в жидкой системе) не вызывает изменений в картине Фурье-преобразования.

7. Выводы

Биомедицинские применения когерентной оптики многочисленны, эффективны, но случайны. Коммерческое использование когерентной оптики не предпринималось, не считая некоторых упомянутых ранее замечательных исключений.

8. Приложение: различные методы формирования трехмерных изображений

О формировании трехмерных изображений было сказано так много, что возможна некоторая путаница. Целью данного приложения является систематизация различных терминов и понятий с тем, чтобы они стали легкими для понимания и сравнения между собой.

Пусть нам дан трехмерный объект, который может содержать и некоторую внутреннюю структуру. Каким образом мы можем его зарегистрировать на двумерном носителе? Существуют четыре основных способа решения этой проблемы. Во-первых, мы можем записать голограмму этого объекта. Голограмма зарегистрирует полную трехмерную информацию об объекте (за исключением теневых эффектов в плоских голограммах, которые исчезают в цилиндрической голограмме). Во-вторых, мы можем сжать одно измерение, чтобы обеспечить правильное изображение в двух измерениях и неясное в третьем. Метод проекций в рентгенотехнике даст хорошие иллюстрации этого. С помощью точечного источника излучения мы можем спроектировать на экран тень объекта (как это показано на рис. 8.1,а). Отметим, что для каждой точки теневого изображения мы можем провести прямую линию, соединяющую эту точку с точечным источником. Распределение поглощения излучения вдоль этой линии оказывается неопределенным (во всяком случае, известно только полное поглощение вдоль этой линии). Обычные рентгеновские изображения имеют именно такой характер. Назовем такие проекции двумерными проекциями (для достижения цели, поставленной в приложении). В отличие от этого один срез двумерной проекции (который мог бы быть получен с помощью расходящегося пучка в виде веера, как показано на рис. 8.1, б), мы назовем одномерной проекцией.

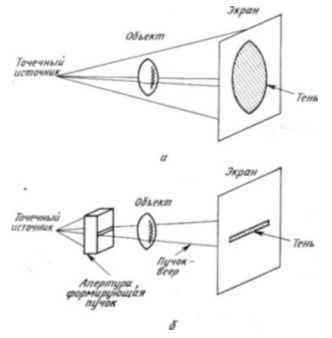
Рис. 8.1.Точечный источник создает конус направленных на объект лучен, которые и образуют на экране его теневое изображение (а). Если между точечным источником и объектом поместить щелевую диафрагму, то объект будет освещаться только веером лучей. В этом случае мы имеем трансаксиальное освещение, показанное на нижнем рисунке (б).

Получив проекции объекта (одно- и двумерные) с многих ракурсов и осуществив восстановление, мы можем синтезировать изображение трехмерного объекта (по его двумерным проекциям) или получить двумерное сечение этого объекта веерным пучком (по его одномерным проекциям). Примерами синтеза трехмерных изображений объекта по его двумерным проекциям являются псевдопараллаксные изображения, а также цилиндрические мультиплексные голограммы. Примером синтеза двумерного изображения объекта по его одномерным проекциям служит трансаксиальная томография. Во всех этих случаях дополнительное измерение синтезируется по многочисленным проекциям, полученным с многих направлений. В-третьих, мы можем совсем не учитывать одну координату из трех. Метод профилирования, является примером такого подхода. Обозначив поперечные координаты через х и у, а координату по глубине через z, получаем профили изображений в координатах х—z при постоянном у и в координатах у—z при постоянном х. И, наконец, в-четвертых, мы можем точно записать изображение в координатах х—у и восстановить затем координату z (измерение по глубине) некоторым образом (например, с помощью контуров по глубине.

 Скачать реферат