Эконометрическое моделирование - расчет коэффициентов корреляции и регрессии, анализ одномерного временного ряда

Уравнение регрессии зависимости цены квартиры от города области и общей площади квартиры, полученное на последнем шаге, можно записать в следующем виде

y = 10,255 - 34,558Х1 + 1,492Х3

Коэффициенты уравнения регрессии показывают, что в Подольске цена квартиры меньше, чем в Люберцах на 34,558 тыс. долл., а при увеличении общей площадина один квадратный метрцена квартиры увеличится на 1,

492 тыс. долл.

7)Оценка качества построенной модели. Оценка влияния значимых факторов на результат с помощью коэффициентов эластичности,  - и  - коэффициентов

Сравним индекс корреляции R и коэффициент детерминации R2 полученной модели с однофакторной моделью.

Таблица 5

Из таблицы (5) видно, что качество новой модели лучше предыдущей однофакторной, т.к. коэффициенты ближе к единице.

Теперь оценим влияние значимых факторов на результат с помощью коэффициентов эластичности, - коэффициентов с помощью формул:

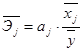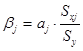, и ,

где

1) = = -0,212

=

Отсюда видно, что при изменении Х1 на 1% значение Y уменьшится на 21,2%. А при изменении Х3 на 1% значение Y увеличится на 110,3%.

2) Найдем коэффициенты β для параметра Х1 и Х3. Сначала вычислим среднеквадратические отклонения:

=

=

=

Тогда:

=

=

Анализ полученных данных показывает, что при увеличении Х1 на 0,5006 цена квартиры уменьшится на 0,336*51,492 = 17,301 тыс. долл. А при увеличении общей площади на 28,225 м2 Цена квартиры увеличится на 0,817*51,492 = 42,07 тыс. долл.

3) Вычислим коэффициенты Δ для параметров Х1 и Х3:

= -0,403 * (-0,336) / 0,827 = 0,164

= 0,846 * 0,817 / 0,827 = 0,836

Из полученных данных мы видим, что доля влияния фактора город (Х1) в суммарном влиянии всех факторов составляет 0,164 или 16,4%, тогда как доля влияния фактора общая площадь – 0,836 или 83,6%.

Задача №2. Исследование динамики экономического показателя на основе анализа одномерного временного ряда

Таблица 6– Исходные данные

1. Выявление аномальных наблюдений

Построим график временного ряда

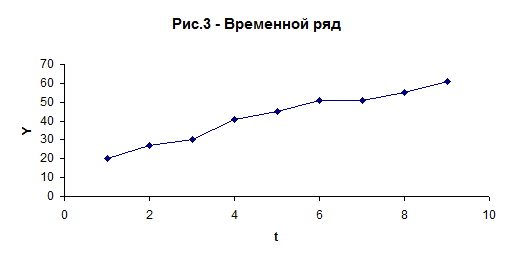
Для выявления аномальных наблюдений воспользуемся методом Ирвина. Для всех наблюдений вычисляем величину по формуле:

,

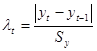Где ,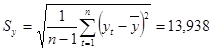

Результаты расчетов по методу Ирвина приведены в таблице (6)

Таблица 6

По результатам расчетов аномальных наблюдений нет, т.к. расчетные величины не превышают табличных значений.

2. Построение линейной модели

Таблица 7 - Промежуточные расчеты параметров линейной модели

 Скачать реферат