Теория игр и статических решений

Решение:

Заменим знаки вопроса на неизвестные переменные следующим образом:

Попытаемся заполнить пропуски в таблице так, чтобы равновесия по Нэшу достигались в вариантах игры (A, a), (B, a), (B, b), а при игре (A, b) равновесие по Нэшу не достигалось. Тогда должна выполняться система неравенств (объедим их парами для каждого варианта игры):

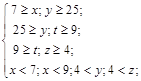Откуда получаем:

Возьмем минимальные целые числа, удовлетворяющие системе неравенств. Получим игру:

Действительно, в данной игре варианты (A, a), (B, a), (B, b) будут являться равновесиями по Нешу, т.к. здесь ни одному из игроков не выгодно изменить свою стратегию, а при игре (A, b) каждому из игроков выгодно изменить свою стратегию.

Найдем равновесие в смешанных стратегиях. Предположим, что первый игрок с вероятностью µ играет стратегию A, соответственно с вероятностью (1 - µ) – стратегию B. Второй игрок с вероятностью ν играет стратегию a, а с вероятностью (1 - ν) - стратегию b. Тогда функции выигрыша игроков будут выглядеть следующим образом:

;

Тогда функции отклика будут следующими:

Имеем 2 равновесия в смешанных стратегиях. Если второй игрок играет стратегию b, то первый игрок всегда будет играть стратегию B. Если первый игрок играет стратегию А, то второй игрок будет играть стратегию a.

Решением же в доминируемых стратегиях будет (B, a).

3. Двое бегут по лыжной трассе навстречу друг другу. У каждого лыжника 2 стратегии: «уступить» (У) и «не уступить» (Н). Если один из игроков уступает другому, то его потери - 9 секунд, второй – не теряет ничего; если же лыжники сталкиваются, то оба теряют 25 секунд.

d) Составьте платежную матрицу этой игры. Найдите равновесия в чистых стратегиях.

e) Нарисуйте линии откликов игроков и найдите смешанные равновесия в этой игре.

f) Допустим теперь, что у игроков теперь 3 стратегии: «не уступить», «уступить» и «уступить пол-лыжни». Если оба уступили друг другу пол-лыжни, то потери каждого 4 секунд, если же один уступил пол-лыжни, а второй - нет, то лыжники столкнутся, и потери при столкновении у уступившего – 29 секунд, у неуступившего - 4 секунды. Найдите все равновесия по Нэшу (в чистых и в смешанных стратегиях).

Решение:

a) Составим платежную матрицу этой игры:

В чистых стратегиях равновесия в данной игре нет.

b) Найдем равновесие в смешанных стратегиях.

Предположим, что первый игрок с вероятностью µ играет стратегию У, соответственно с вероятностью (1 - µ) – стратегию Н. Второй игрок с вероятностью ν играет стратегию У, а с вероятностью (1 - ν) - стратегию Н.

Функции выигрыша игроков:

Соответственно функции откликов:

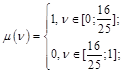
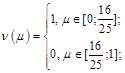
Имеем 2 точки пересечений линий, соответствующие равновесиям в смешанных стратегиях:

2. (Н; У), то есть первый игрок всегда не уступает, а второй – уступает;

3. (У; Н), то есть первый игрок всегда уступает, а второй – не уступает;

4. Каждый из игроков с вероятность 16/25 уступает лыжню и с вероятностью 9/25 не уступает лыжню.

c) Составим платежную матрицу игры:

В чистых стратегиях равновесия нет.

4. Профсоюз заключает с фирмой соглашение на несколько лет об уровне заработной платы w>0. Профсоюз максимизирует функцию совокупной прибыли членов профсоюза (зарплата за вычетом издержек от работы): u(w,L)=wL-4*L2, фирма максимизирует свою прибыль (выпуск за вычетом зарплаты): П(w,l)=7*L0.5-wL.

d) Найти равновесный уровень заработной платы и занятости в статической игре.

e) Каково равновесие в динамической игре, если профсоюз достаточно мощный, чтобы навязать фирме любой уровень заработной платы, после чего фирма не может менять уровень заработной платы в течение срока контракта, но может нанимать любое количество труда L>0.

f) Каково равновесие в динамической игре, если фирма – монополист на рынке труда, и она может установить любую заработную плату, после чего профсоюз может только регулировать численность работающих на монополиста.

Решение:

b) Профсоюз устанавливает уровень заработной платы. В свою очередь исходя из этого значение фирма определяет количество занятых. Предположим, что профсоюз установил уровень заработной платы w*. Тогда прибыль фирмы будет П(w*,l)=7*L0.5- w*L. Максимизируем прибыль по L.

 Скачать реферат