Прогноз годовой прибыли

Средняя относительная ошибка аппроксимации определяется по приближенной формуле:

Sрег

Eотн≈0,8 · — · 100%=0.8 · 2.252208/66.9 · 100%≈2.7

− y

где тыс. руб. — среднее значение продолжительности жизни (определено с помощью встроенной функции «СРЗНАЧ»; прил. 1).

Еотн пок

азывает, что предсказанные уравнением регрессии значения годовой прибыли Y отличаются от фактических значений в среднем на 2,7 %. Модель имеет высокую точность (при — точность модели высокая, при — хорошая, при — удовлетворительная, при — неудовлетворительная).

5.Для экономической интерпретации коэффициентов уравнения регрессии сведем в таблицу средние значения и стандартные отклонения переменных в исходных данных (табл. 4). Средние значения были определены с помощью встроенной функции «СРЗНАЧ», стандартные отклонения — с помощью встроенной функции «СТАНДОТКЛОН» (см. прил. 1).

Таблица 4

Средние значения и стандартные отклонения используемых переменных

1) Фактор X1 (ВВП в паритетах покупательной способности)

Значение коэффициента b1=0,044918 показывает, что рост ВВП в паритетах покупательной способности на 1 %. приводит к повышению средней ожидаемой продолжительности жизни при рождении на 0,044918 лет.

Средний коэффициент эластичности фактораX1 имеет значение

x1 29.75

Е1= b1 · ― = 0.044918 · ≈ 0.01997

y 66.9

Он показывает, что при увеличении ВВП в паритетах покупательской способности на 1 % годовая прибыль увеличивается в среднем на 0,01997 %.

2) Фактор X4 (коэффициент младенческой смертности)

Значение коэффициента b4=(-0,24031) показывает, что рост коэффициента младенческой смертности на 1 %. приводит к уменьшению средней ожидаемой продолжительности жизни при рождении в среднем на -0,24031 лет.

Средний коэффициент эластичности фактораX4 имеет значение

x4 40.9

Е4 = b4 · ― = - 0.24031 · ≈ 0.1469

y 66.9

Он показывает, что при увеличении коэффициента младенческой смертности на 1 % средняя ожидаемая продолжительность жизни увеличивается в среднем на 0,1469 %.

Средний коэффициент эластичности для фиктивных переменных лишен смысла, поэтому не рассчитывается.

Сравним между собой силу влияния факторов, включенных в регрессионную модель, на годовую прибыль, для чего определим их бета–коэффициенты:

Sx1 28.76

B1 = b1 · ― = 0.044918 · ≈ 0.1346;

Sy 9.6

Sx4 3 4.8

B4 = b4 · ― - 0.24031 · ≈ - 0.8711

Sy 9.6

Сравнивая по абсолютной величине значения бета–коэффициентов, можно сделать вывод о том, что на изменение средней ожидаемой продолжительности жизни при рождении Y сильнее всего влияет ВВП в паритетах покупательской способности Х1, далее по степени влияния следует коэффициент младенческой смертности Х4.

Определим дельта–коэффициенты факторов:

ry,x1 0.780235

Δ1 = B1 · _ = 0.1346 · _ ≈ 0.11094;

R2 0.946585

ry,x4 - 0.96876

Δ4 = B4 · _ = - 0.8711 · _ ≈ 0.8915;

R2 0.946585

где ry,x1=0,780235; ry,x4=(–0,96876); — коэффициенты корреляции между парами переменных Y–X1 и Y–X4 соответственно (см. табл. 1); R2=0,946585 — множественный коэффициент детерминации (см. табл. 3).

Сумма дельта–коэффициентов факторов, включенных в модель, должна быть равна единице. Небольшое неравенство может быть вызвано погрешностями промежуточных округлений.

Таким образом, в суммарном влиянии на среднюю ожидаемую продолжительность жизни при рождении Y всех факторов, включенных в модель, доля влияния ВВП в паритетах покупательной способности X1 составляет 11,094 %, коэффициента младенческой смертности Х4 — 89,15 %.

6.Рассчитаем прогнозное значение годовой прибыли, если прогнозные значения факторов составят 75 % от своих максимальных значений в исходных данных. Максимальные значения факторов были определены с помощью встроенной функции «МАКС» (см. прил. 1). Прогнозные значения рассчитываются только для количественных факторов X1 и X4:

· фактор Х1: х01=0,75*х1max=0.75*100=75;

· фактор Х4: x04=0.75*x4max=0.75*124=93.

Среднее прогнозируемое значение (точечный прогноз) годовой прибыли государственной компании (x06=0) составляет:

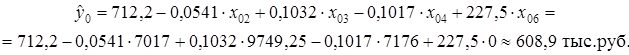
Для частной компании (x06=1) этот показатель равен

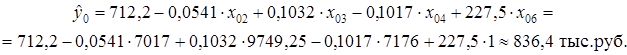
Стандартная ошибка прогноза фактического значения годовой прибыли y0 рассчитывается по формуле

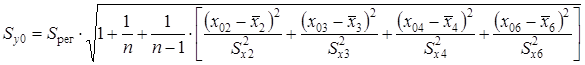
Так как фиктивная переменная Х6 может принимать два значения — 0 или 1, то Sy0 определяется для обоих случаев:

· для государственных компаний (x06=0):

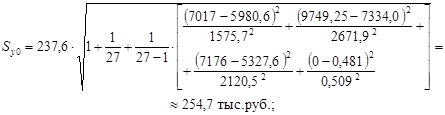
· для частных компаний (x06=1):

Построим интервальный прогноз фактического значения годовой прибыли y0 с доверительной вероятностью g=0,8. Доверительный интервал имеет вид:

,

где tтаб=1,321 — табличное значение t-критерия Стьюдента при уровне значимости и числе степеней свободы (p=4 — число факторов в модели) (см. Справочные таблицы).

Для государственных компаний:

тыс. руб.

Таким образом, с вероятностью 80 % годовая прибыль государственных компаний при заданных значениях факторов будет находиться в интервале от 272,4 до 945,4 тыс. руб.

Для частных компаний:

тыс. руб.

 Скачать реферат