Основы практического использования прикладного регрессионного анализа

(3.1)

и дисперсией

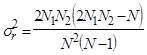(3.2)

Здесь – число наблюдений со знаком (+), – число наблюдений со знаком (–).

Когда ght=20 src="images/referats/5458/image071.png">соотношения (3.1) и (3.2) принимают вид

Для решения второй подзадачи используется метод последовательных разностей. Элементы исследуемой выборки располагаются в порядке получения наблюдений и для них вычисляются выборочные среднее и дисперсия

Определяют разности между соседними наблюдениями

и математическое ожидание квадрата разности

где – оценка генеральной дисперсии.

Фактическая величина критерия случайности выборки

.

Теоретическое значение критерия

При для конкретного N гипотеза случайности отвергается.

1.2.2 Проверка стационарности

Анализ случайных процессов может производиться осреднением величин по ансамблю выборочных реализаций или по одной реализации.

Поскольку на практике проверка по ансамблю достаточно длинных выборочных реализаций неосуществима, то для использования тестов проверки стационарности процесса принимается ряд допущений:

а) проверка заключается в исследовании поведения не ансамбля, а его отдельных реализаций; это означает, что доказательство внутренней стационарности отдельных реализаций может служить доказательством стационарности случайного процесса, которому принадлежит эта реализация;

б) для большинства процессов достаточно проверить слабую стационарность, поскольку, во-первых, для эффективного использования спектрального и корреляционного анализа случайных процессов достаточно выполнения условия слабой стационарности, а во-вторых, для реальных процессов обычно слабая стационарность влечет за собой и строгую; если процесс определяется нормальной плотностью, то это доказательство осуществляется автоматически, поскольку все моменты высших порядков полностью определяются средним и автокорреляционной функцией;

в) на практике часто стационарность автокорреляционной функции обеспечивается стационарностью дисперсии.

Учитывая эти допущения, проверку стационарности осуществляют исследованием одной реализации .

Для этого реализация делится на N равных интервалов таких, что её участки в пределах каждого интервала можно считать независимыми. Для всех интервалов вычисляются средние значения и средние значения квадратов, из которых составляются две последовательности и затем их проверяют на наличие тренда.

Если известно выборочное распределение, то для проверки можно использовать существующие непараметрические критерии (t-критерий Стьюдента, -критерий Пирсона, F-критерий Фишера), однако в обычной ситуации проверка стационарности осуществляется при высокой неопределенности относительно исследуемого процесса. В этом случае целесообразно использовать непараметрические критерии, например, критерий серий и критерий тренда

Критерий тренда основан на подсчете числа случаев, когда для в последовательности N наблюденных значений величины x.

Такое неравенство называется инверсией, а их число k определяется из соотношения

,

где

Число инверсий есть также случайная величина со средним

и дисперсией

.

Область принятия гипотезы ограничена интервалом .

Критерий тренда обладает большей мощностью при выявлении монотонного тренда, однако при выявлении колебательного тренда его мощность невелика, в этом случае целесообразнее использовать критерий серий.

Критерии проверки гипотезы стационарности обладают рядом особенностей:

1) Нет необходимости знать ширину полосы частот исследуемых процессов;

2) Не требуется точно знать время осреднения, использованное для вычисления средних и квадратов отклонений от средних;

3) Для проверки не обязательно, чтобы исследуемые процессы были полностью случайными. При изучении процессов может возникнуть случай, когда независимость от времени средних и квадратов не является достаточным условием для утверждения о независимости от времени автокорреляционной функции.

1.3 Обнаружение выбросов в выборке

Выбросом среди остатков представляет собой остаток, который значительно превосходит по абсолютной величине остальные и отличается от среднего по остаткам на три, четыре или даже более стандартных отклонений.

Для обнаружения выбросов необходимо построить график остатков, определённых по формуле

В случае если , данная точка будет характеризовать выброс. Следует отметить, что иногда выброс может дать полезную информацию. В этом случае необходимо более тщательное исследование выбросов, а не механическое их отбрасывание. Выбросы должны быть исключены сразу если выясняется, что они вызваны такими причинами, как ошибки в регистрации данных, неудовлетворительная настройка аппаратуры и т.д. Если имеется не одно аномальное измерение, то критерий их не обнаруживает, особенно если анализируется менее 30 измерений.

1.4 Мультиколлинеарность переменных

Одно из основных предположений регрессионного анализа относится к матрице исходных данных: среди независимых переменных не должно быть линейно зависимых. Это требование необходимо для вычисления оценки методом наименьших квадратов.

 Скачать реферат