Основы практического использования прикладного регрессионного анализа

а) Получение наилучших точечных и интервальных оценок неизвестных параметров регрессионного анализа;

б) Проверка гипотез относительно этих параметров;

в) Проверка адекватности;

г) Проверка множества предполагаемых предположений.

Исследуемый объект представлен на рисунке 3.2

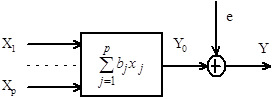
Рисунок 1.2 — Вид исследуемого о

бъекта

Для корректного использования регрессионного анализа существует следующие предпосылки и следующие допущения на свойства регрессионной ошибки , ; - значение зависимой переменной, полученное подстановкой в уравнение , , ; - количество экспериментальных данных, - количество независимых переменных:

Приведем свойства и предпосылки регрессионной ошибки:

а) Свойства регрессионной ошибки:

1) В каждом опыте имеет нормальный закон распределения;

, .

2) В каждом опыте математическое ожидание равно нулю;

, .

3) Во всех опытах дисперсия постоянна и одинакова;

, .

4) Во всех опытах ошибки независимы.

, .

б) предпосылки регрессионной ошибки:

1). Матрица наблюдений имеет полный ранг;

.

2). Структура модели адекватна истинной зависимости;

3). Значения случайной ошибки не зависят от значений регрессоров ;

4). Ошибки регистрации регрессоров пренебрежимо малы по сравнению со случайной ошибкой .

1.2 Проверка предпосылок и предположений регрессионного анализа

Регрессионный анализ является одним из самых распространённых методов обработки результатов наблюдений. Он служит основой для целого ряда разделов математической статистики и методов обработки данных. Регрессионный анализ базируется на ряде предположений и предпосылок, нарушение которых приводит к некорректному его использованию и ошибочной интерпретации результатов.

Если F-критерий и показал, что подгонка модели в целом является удовлетворительной; целесообразно провести анализ остатков для проверки соблюдений предпосылок и предположений.

В этом случае исследуется набор отклонений между экспериментальными и предсказанными значениями зависимой переменной,

.

Проверка предпосылок и предположений регрессионного анализа включает в себя следующие задачи:

1) оценка случайности зависимой переменной;

2) оценка стационарности и эргодичности зависимых и независимых переменных;

3) Проверка гипотезы о нормальности распределения ошибок E;

4) Обнаружение выбросов;

5) Проверка постоянства математического ожидания и дисперсии ошибок;

6) Оценка коррелированности остатков;

7) Обнаружение мультиколлинеарности.

1.2.1 Проверка случайности

Построение моделей методом множественного регрессионного анализа требуется выполнение предположения случайности и в нормальной линейной модели вида

где – вектор наблюдений зависимой переменной;

– матрица наблюдений независимых переменных;

– вектор неизвестных коэффициентов;

– вектор ошибок.

Задача проверки случайности может быть разбита на 2 подзадачи:

1) проверка случайности собственной величины Y;

2) проверка случайности выборки, то есть допущения об отсутствии существенного смещения средней величины во времени.

Первая подзадача решается с использованием критерия серий. Для этой цели последовательность наблюдений величины Y представляют последовательностью нулей и единиц, где единицей обозначают значение, превышающее среднее или медиану, и нулем, собственно, значение меньшее медианы. После обозначения вектор наблюдений преобразуется в последовательность серий где – количество подряд идущих элементов одного вида, i – номер серии.

Доказано, что при распределение величины r близится к нормальному с характеристиками

Тогда с вероятностью 0,954 теоретическое число серий r будет находиться в пределах

Если фактическое значение попадает в указанные пределы, то Y можно считать случайной величиной.

Серией называется последовательность наблюдаемых значений, перед которыми и после которых расположены наблюдаемые значения другой категории. Если последовательность N наблюдений представляет собой независимые наблюденные значения одной и той же случайной величины, т.е. вероятность знаков (+) и (–) не меняется от одного наблюдения к другому, то выборочное распределение числа серий в последовательности есть случайная величина r со средним значением

 Скачать реферат