Формирование понятия функции в курсе математики средней школы
а) y2 = x2; б) y = x2; в) y = lg x; г) y = ![]() .
.
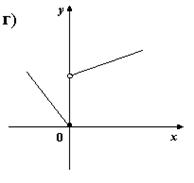
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
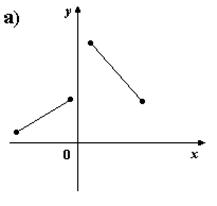
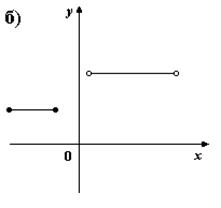
ht=216 src="images/referats/7456/image135.jpg">
3) Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x)) ?
а) f(x) = tg(x), g(x) = arctg x; б) f(x) = ![]() , g(x) = x3;
, g(x) = x3;
в) f(x) = x2, g(x) = ![]() ; г) f(x) =
; г) f(x) = ![]() , g(x) = x2.
, g(x) = x2.
4) Даны функции f(x) = x2 и g(x) = ![]() . Какая запись в таком случае верна?
. Какая запись в таком случае верна?
а) f(g(x)) = (![]() )2; б) f(g(x)) =
)2; б) f(g(x)) = ![]() ;
;
в) f(g(x)) = |x|; г) f(g(x)) = x.
5) На каком из рисунков изображен график четной функции?
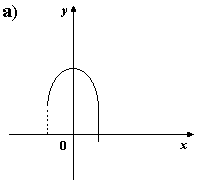
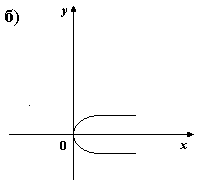
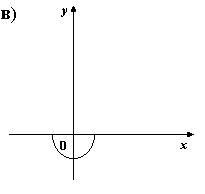
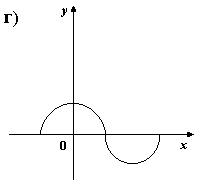
6. Укажите четную функцию.
а) y = sin (2x+1); б) y = sin (x2+1);
в) y = cos (x2+1); г) y = x+cos x.
7. Укажите нечетную функцию.
а) f(x) = x3 +1; б) f(x) = 2x – 2-x;
в) f(x) = 2x + 2-x; г) f(x) = ![]()
8. Какое высказывание ложно?
а) Сумма двух четных на R функций есть функция четная.
б) Разность двух четных на R функций есть функция четная.
в) Произведение двух четных на R функций есть функция четная.
г) Всякая функция есть функция четная, либо нечетная.
9. Какие из данных множеств могут быть областями определения периодических функций?
а) (-¥; +¥); б) (0;+¥); в) множество всех чисел, кроме чисел вида pk, где k = 0, ±1, ±2, …
10. Какая из функций обладает следующими свойствами:
существует такое t ¹ 0, что при любом x из области определения выполняется равенство f(x+t) = f(x)?
а) y = ![]() ; б) y = x2; в) y = sin
; б) y = x2; в) y = sin ![]() ; г) y = x sin x.
; г) y = x sin x.
11. Какая из функций не является периодической?
а) y = sin(x+1);
б) y = cos x + tg x;
в) y = x + sin x;
г) y = {x}.
12. Какая из функций имеет период ![]() ?
?
а) y = tg x – ctg x; б) y = sin 2x;
в) y = cos ![]() ; г) y = sin x + cos x.
; г) y = sin x + cos x.
Вариант II
1. Какое равенство задает отношение, при котором каждому значению x соответствует не более одного значения y?
а) y2 = x2; б) x2y2 = 1; в) ![]() = x; г) sin y = x.
= x; г) sin y = x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
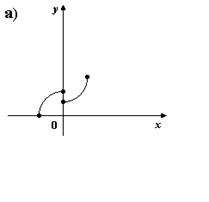
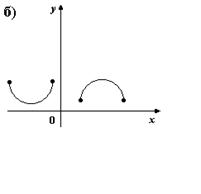
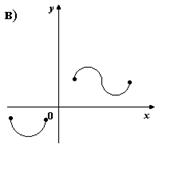
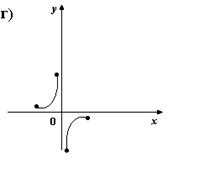
3. Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x))?
а) f(x) = sin x, g(x) = arcsin x; б) f(x) = arcsin x, g(x) = sin x;
в) f(x) = ex, g(x) = ln x; г) f(x) = ln x, g(x) = ex.
Даны функции f(x) = ![]() и g(x) = x2. Какая запись не верна?
и g(x) = x2. Какая запись не верна?
а) f(g(x)) = ![]() ; б)f(g(x)) =
; б)f(g(x)) = ![]() ;
;
в) f(g(x)) = ![]() ; г) f(g(x)) = (
; г) f(g(x)) = (![]() )2;
)2;
4. На каком из рисунков изображен график четной функции?
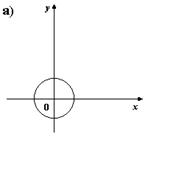
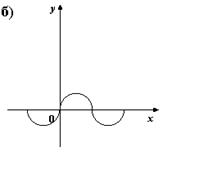

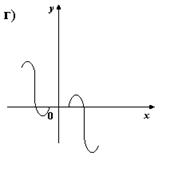
5. Укажите четную функцию.
а) y = x2 – x; б) y = 2x – 2-x;
в) 2x + 2-x; г) y = ![]() .
.
6. Укажите нечетную функцию.
а) f(x) = cos x + sin x; б) f(x) = sin x + tg x;
в) f(x) = cos x + sin x; г) f(x) = tg x×ctg x.
7. Какое высказывание ложно?
а) Сумма двух нечетных функций на R есть функция нечетная.
б) Разность двух нечетных функций на R есть функция нечетная.
в) Произведение двух нечетных функций на R есть функция нечетная.
г) Произведение трех нечетных функций на R есть функция нечетная.
8. Какие из данных множеств могут быть областями определения периодических функций?
а) R – множество действительных чисел;
б) (-2; +¥); в) R \ {2pk, k Î Z0}.
9. Какая из функций обладает следующим свойством:
существует такое t ¹ 0, что при любом x из области определения верно равенство f (x+t) = f(x)?
а) y = x3; б) y = ![]() ; в) y = x cos x; г) y = sin (
; в) y = x cos x; г) y = sin (![]() ).
).
10. Какая из функций не является периодической?
а) y = sin x + ctg x; б) y = cos (2x+1);
в) y = sin (![]() )2; г) y = sin x×tg x.
)2; г) y = sin x×tg x.
11. У какой функции наименьший положительный период больше 2p?
а) y = sin x + ![]() sin 2x +
sin 2x + ![]() sin 3x;
sin 3x;
б) y = 3 tg ![]() ;
;
в) y = tg x + ctg ![]() ;
;
г) y = sin2 x.
Вариант III
1. Какое равенство задает отношение, при котором некоторым значениям x соответствует более одного значения y?
а) y = arctg x; б) y = tg x; в) tg y = x; г) arctg y = x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое можно рассматривать как график функции?
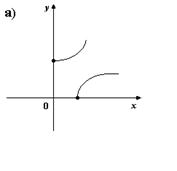
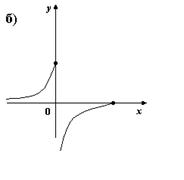
Другие рефераты на тему «Математика»:
- Решение военно-логистических задач по выбору оптимального маршрута для военно-транспортных средств
- Лист Мебиуса
- Статистическое наблюдение, первоначальная обработка и представление ее данных
- Применение уравнение Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы
- Некоторые вопросы геометрии Лобачевского на модели Пуанкаре
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
