Мутации структуры белковоподобного сополимера. Компьютерное моделирование

Рассмотрим зависимости величин индекса Шеннона и размера сжатого файла от энергетического параметра eР при t/t = 500.

Рис. 4.8. зависимости размера сжатого файла LB (a) индекса Шеннона I (b) от энергетического параметра eР (t = 1 млн. шагов интегрирования).

Из рис. 4.8. видно, что в режиме I при eР < 0.2 индекс Ше

ннона и размер сжатого файла более сильно зависит от энергетического параметра, чем в режиме II. Это связано с тем, что при eР < 0.2 происходит вырождение глобулы и образование структуры типа "головастик". Образование длинного «хвоста» ведёт к быстрому снижению значений этих характеристик. Напротив, в режиме II происходит увеличение длин петель. Поэтому зависимость теоретико – информационных характеристик имеет менее выраженный характер.

5. Заключение

1. В процессе эволюции белково-подобного сополимера происходит увеличение длин петель и «хвостов».

2. Теоретико- информационные (индекс Шеннона и размер сжатого файла.) характеристики резко снижают своё значение в процессе эволюции.

3. Для исследованной модели энергия взаимодействия eР » 0.2 разграничивает области устойчивого и неустойчивого состояний.

4. Изучена морфология структур, образующихся в результате эволюции. Устойчивое состояние – мицеллоподобная структура. Вырожденное состояние – структура типа «головастик», в котором Н- звенья образуют ядро, а Р- звенья – хвост.

5. Существует 2 режима молекулярной эволюции. Режим I при eр < 0.2 происходит вырождение глобулы и образование структуры типа «головастик». В связи с образованием длинного «хвоста» индекс Шеннона и размер сжатого файла сильно зависят от энергетического параметра eР. В режиме II образуется мицеллоподобная структура и в основном происходит увеличение петель. Поэтому зависимость теоретико-информационных характеристик от энергетического параметра менее выражена, чем в режиме I.

6. Список литературы

1. Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука, 1989.

2. П. Де Жен Идеи скейлинга в физике полимеров. М.: Мир, 1971.

3. Немухин А.В. Компьютерное моделирование в химии // Соросовский образовательный журнал. 1998. №6. С.48.

4. В.В. Новиков, И.А. Фёдоров. Молекулярно-динамическая модель эволюции белково-подобного сополимера.// Физико – химия полимеров. Синтез, свойства и применение. Выпуск №8.

5. Ю.Г. Папулов, П.Г. Халатур. Конформационные расчёты. Учебное пособие. – Тверь.: КГУ, 1980. –87 с.

6. Термодинамические расчёты. /Р.А. Зимин, Ю.Г. Папулов, Э.А. Серёгин и др. – Калинин: КГУ, 1985. – 87 с.

7. П.Г. Халатур, А.Р. Хохлов. Компьютерное моделирование полимеров//Соросовский образовательный журнал, том 7, №8, 2001. с. 1-8.

8. А.Р. Хохлов, С.И. Кучанов. Лекции по физической химии полимеров. – М.: Мир, 2000. –189 с.

9. Д.Г. Ширванянц, П.Г. Халатур. Компьютерное моделирование полимеров: Учеб. пособие. – Тверь: Твер. гос. ун-т, 2000. – 155 с.

10. Yu. Grosberg and A. R. Khokhlov, Giant Molecules: Here and There and Everywhere. _Academic Press, New York,1993.

11. _ A. Yu. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules _AIP, New York, 1994_.

12. Anders Irbacka, Erik Sandelinb. Monte Carlo study of the phase structure of compact polymer chains.// Journal of chemical physics Vol. 110, Number 24, 1999. pp. 12256 – 12262.

13. P. G. Khalatur, Computer simulation of self-associating polymer systems./Polymer Science,vol. 42, No. 2, 2000. pp. 229-260.

14. Pavel G. Khalatur , Viktor V. Novikov 2, Alexei R. Khokhlov–Conformation – dependent evolution of copolymer sequences.//Physical review E 67, 0519XX. –pp. 1-10.

15. P.G. Khalatur, A.R. Khohlov//Molecular Phys. 1998.V. 93, №4. p. 555.

16. P.G. Khalatur, L.V. Zherenkova, A.R. Khohlov.// Europ. Phys. J. 1998. V. 5B, №4. P. 881.

17. A.R.Khokhlov, P.G.Khalatur. Protein-like copolymers: computer simulation.//Physica A 249, 253 (1998).

18. A.R.Khokhlov, P.G.Khalatur, Phys. Rev. Lett. 82, 3456 (1999).

19. A.R.Khokhlov, P.G.Khalatur, V.A. Ivanov, A.V. Cherovich, A.A. Lazutin Conformation-dependent sequence design: a review of the method and recent theoretical and computer results//Challenges in molecular simulation,. 2002 . pp. 79-99

20. Yuri A. Kriksin, 1 Pavel G. Khalatur, Alexei R. Khokhlov. Reconstruction of Protein-Like Globular Structure for Random and Designed Copolymers//Macromol. Theory Simul. 2002, 11, 213-221

21. E. I. Shakhnovich and A. M. Gutin, Proc. Natl. Acad. Sci.U.S.A. 90, 7195 _1993_.

22. E. I. Shakhnovich and A. M. Gutin, Protein Eng. 6, 793_1993_.

23. V. S. Pande, A. Yu. Grosberg, and T. Tanaka, Proc. Natl. Acad. Sci. U.S.A. 91, 12972 _1994_.

24. E. I. Shakhnovich, Fold Des 3, R45 _1998_.

25. E.A.Zheligovskaya, P.G.Khalatur, A.R.Khokhlov, Phys. Rev. E 59, 3071 (1998).

Приложение 1

Типичное распределение Р и Н мономерных звеньев вдоль цепи белковоподобного сополимера с L = 3.173, случайного сополимера с L = 1.984 и случайно-блочного с L = 3.173. Р - звенья обазначены как –1, Н – звенья как +1. Длина цепи N = 512. [3]

Приложение 2

Зависимости <U/N> и <m> от температуры для 512-звенной цепи белковоподобного сополимера ( L = 3.173), случайный сополимер

(L = 1.084), случайно-блочный сополимер (L = 3.173). [3]

Приложение 3

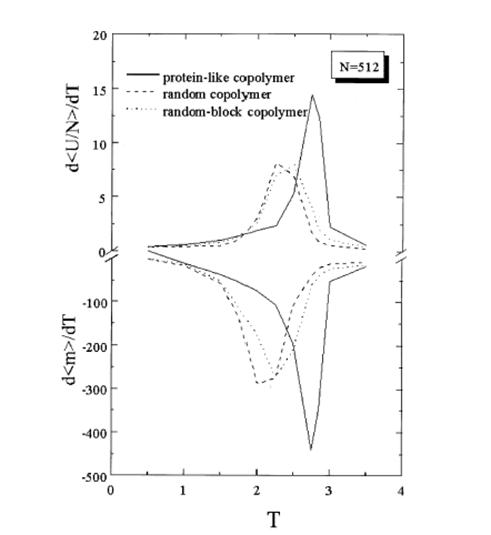
Температурные зависимости d<U/N>/dT и d<m>/dT для 512-звенной гетерополимерной цепи. [3]

Приложение 4

Типичные мгновенные фотографии (Snapshots) глобулярных структур (а) белковоподобных сополимеров ( L = 3.173), (b) случайных сополимеров (L = 1.984), и (c) случайноблочных сополимеров ( L = 3.173) при температуре Т = 1.5 и N = 512. Гидрофобные звенья Н – серые блоки, гидрофильные звенья Р – тёмные блоки. [3]

Приложение 5

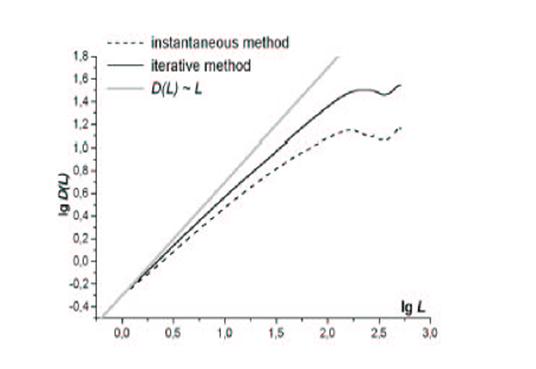
Зависимости DL от L для метода однократного модифицирования поверхности и для итеративного метода (N = 1024). [19]

 Скачать реферат